■テーマ
GeoGebraで関数グラフ
数学WebアプリGeoGebraを使って
関数グラフを描いてみよう
GeoGebraはWebアプリ
だれでもカンタンに数学ができます
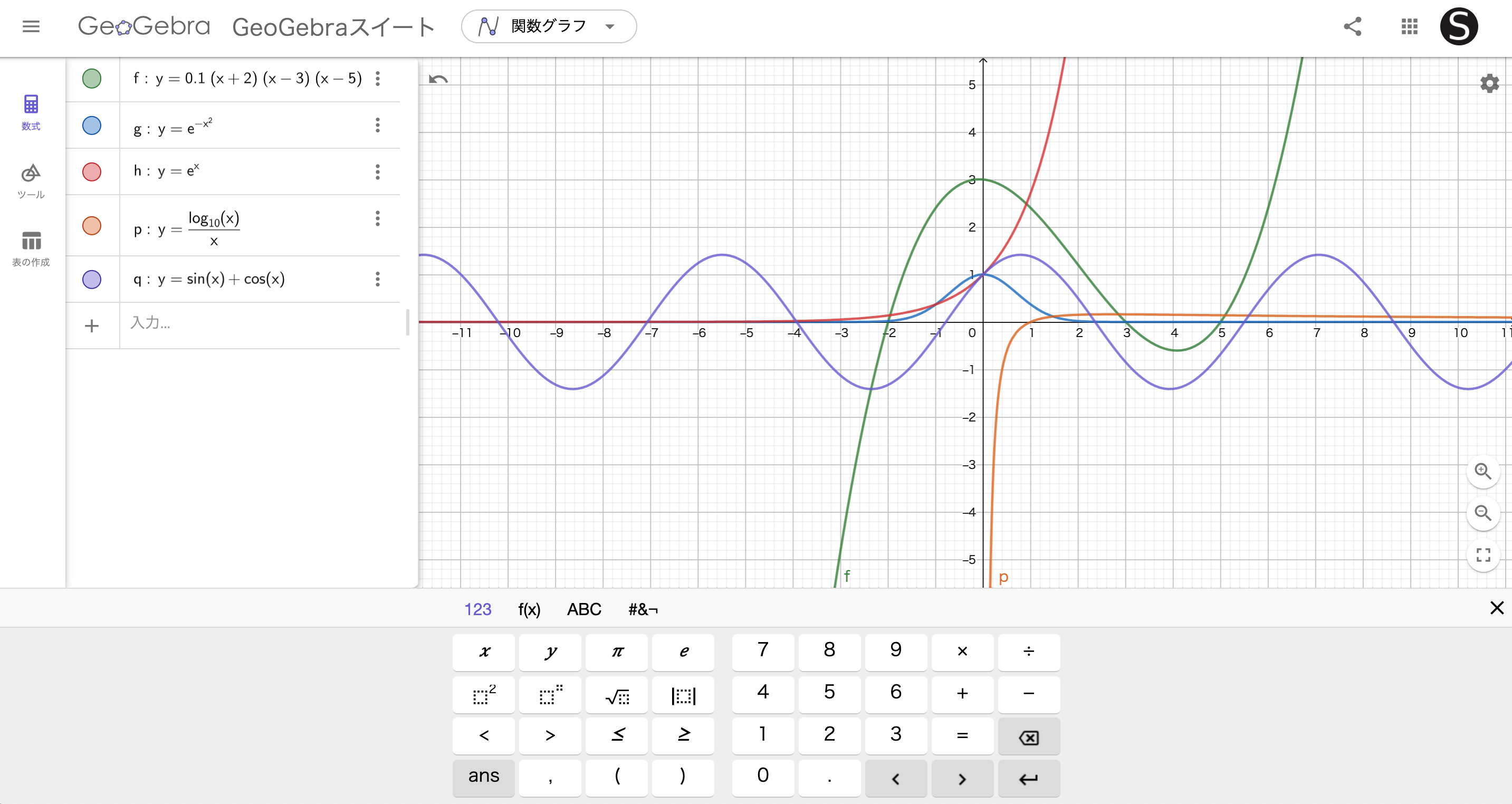
今回は関数グラフを使って
さまざまな式を入力して
どんなグラフになるのかをためしてみます
1行数式グラフコンテスト
〜1行の数式でどれだけ面白いグラフが出力できるか

■Peatix
http://ptix.at/sVM6uN

サイエンスナビゲーター(R)桜井進
■テーマ
GeoGebraで関数グラフ
数学WebアプリGeoGebraを使って
関数グラフを描いてみよう
GeoGebraはWebアプリ
だれでもカンタンに数学ができます
今回は関数グラフを使って
さまざまな式を入力して
どんなグラフになるのかをためしてみます
1行数式グラフコンテスト
〜1行の数式でどれだけ面白いグラフが出力できるか



■Peatix
http://ptix.at/sVM6uN
■対象
小学1年生以上、親子で参加
■テーマ
GeoGebraで関数グラフ
数学WebツールGeoGebraを使って
関数のグラフを描いてみよう
GeoGebraはWebアプリ
だれでもカンタンに数学ができます
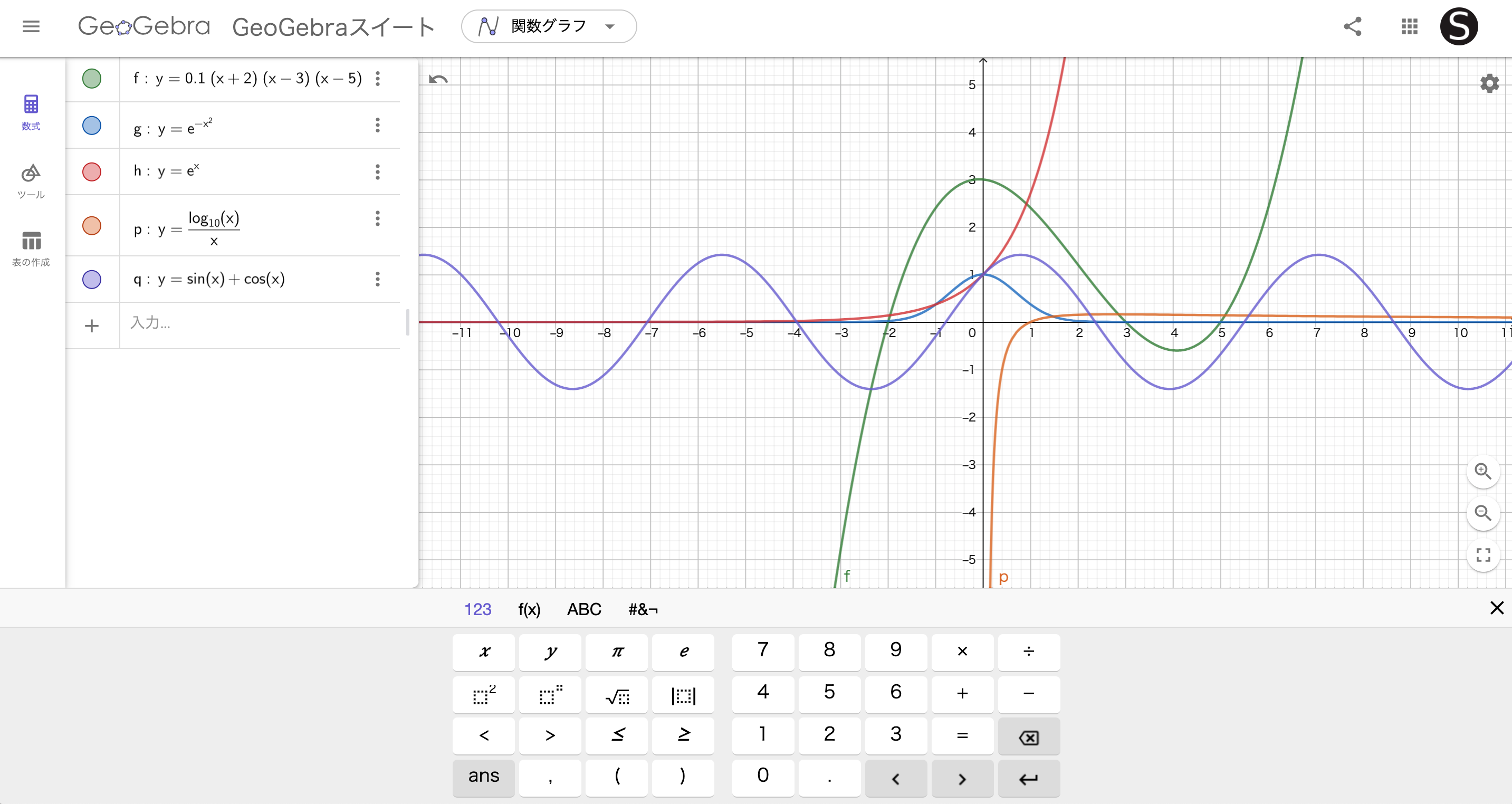
今回は関数グラフを使って
さまざまな式を入力して
どんなグラフになるのかをためしてみます
1行数式グラフコンテスト
〜1行の数式でどれだけ面白いグラフが出力できるか

■Peatix
http://ptix.at/LW75vI
2月20日(日)11:00-12:00 桜井進のPython・UNIX・Math教室(応用コース)
■テーマ
Pythonで自分だけのグラフ計算機をつくる
1行数式グラフコンテスト
〜1行の数式でどれだけ面白いグラフを出力できるか〜
グラフ計算機アプリは山ほどありますが
Pythonをグラフ計算機に使わない手はありません
自分だけの最強のグラフ計算機をデザインします
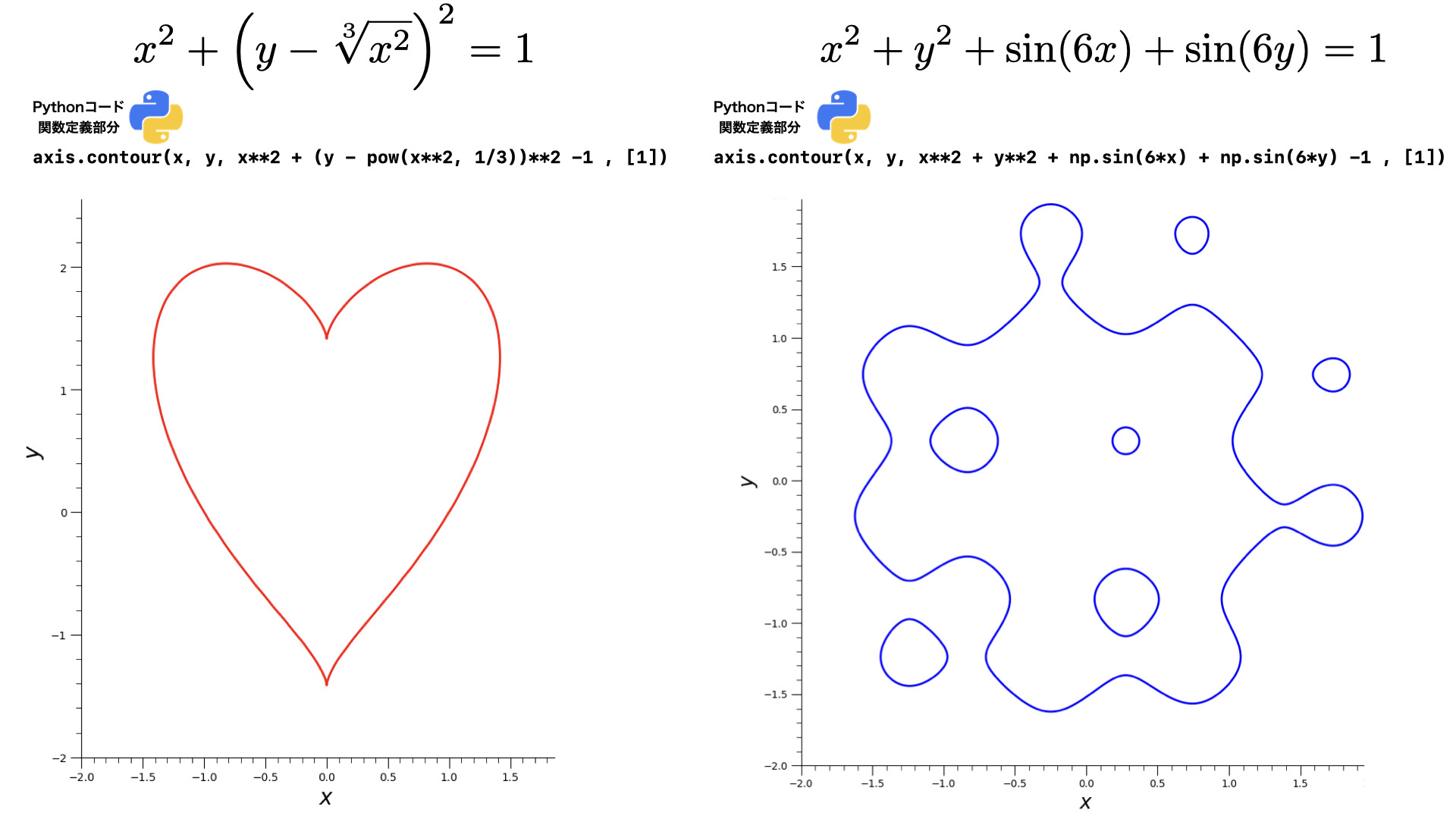
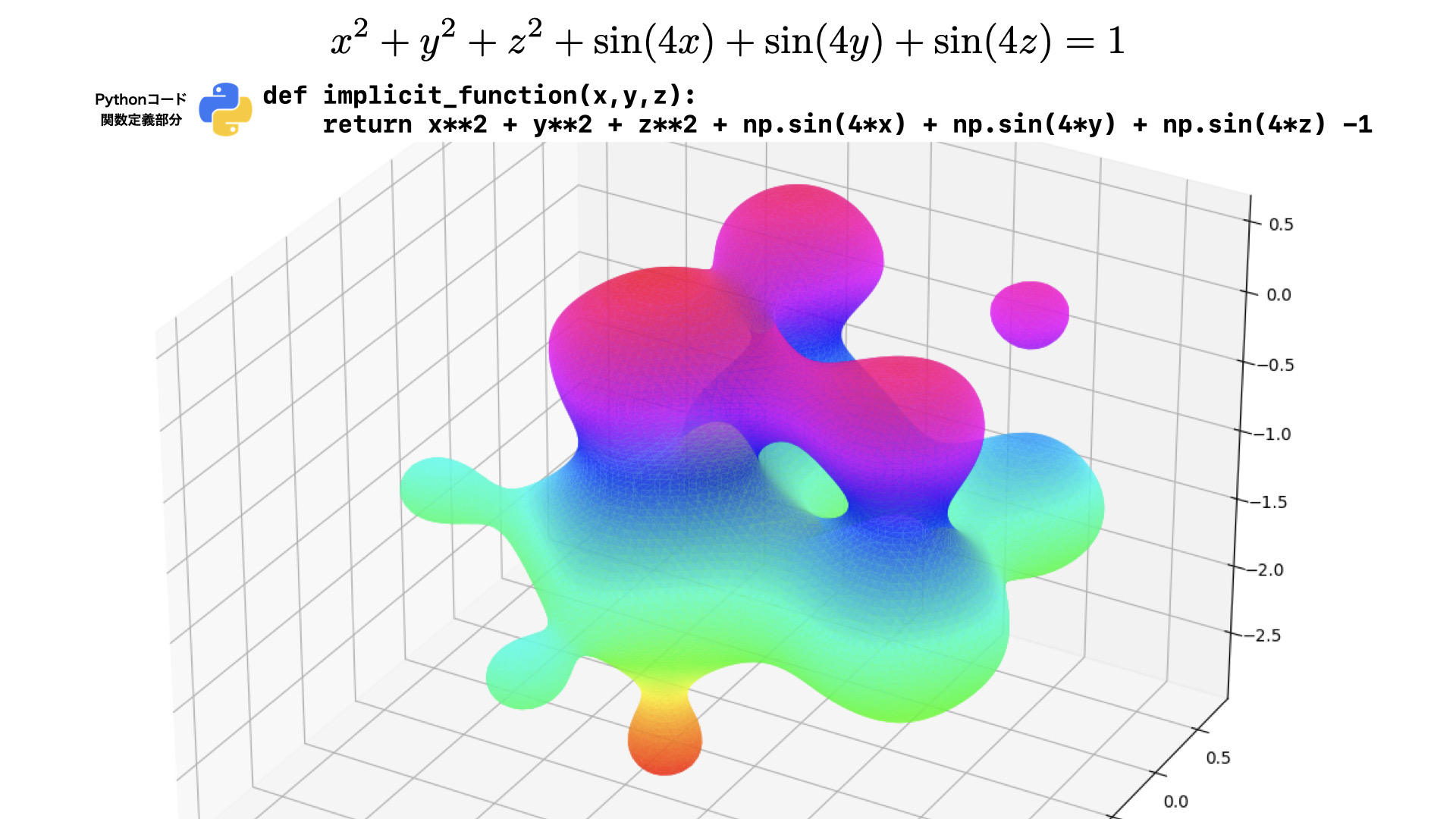
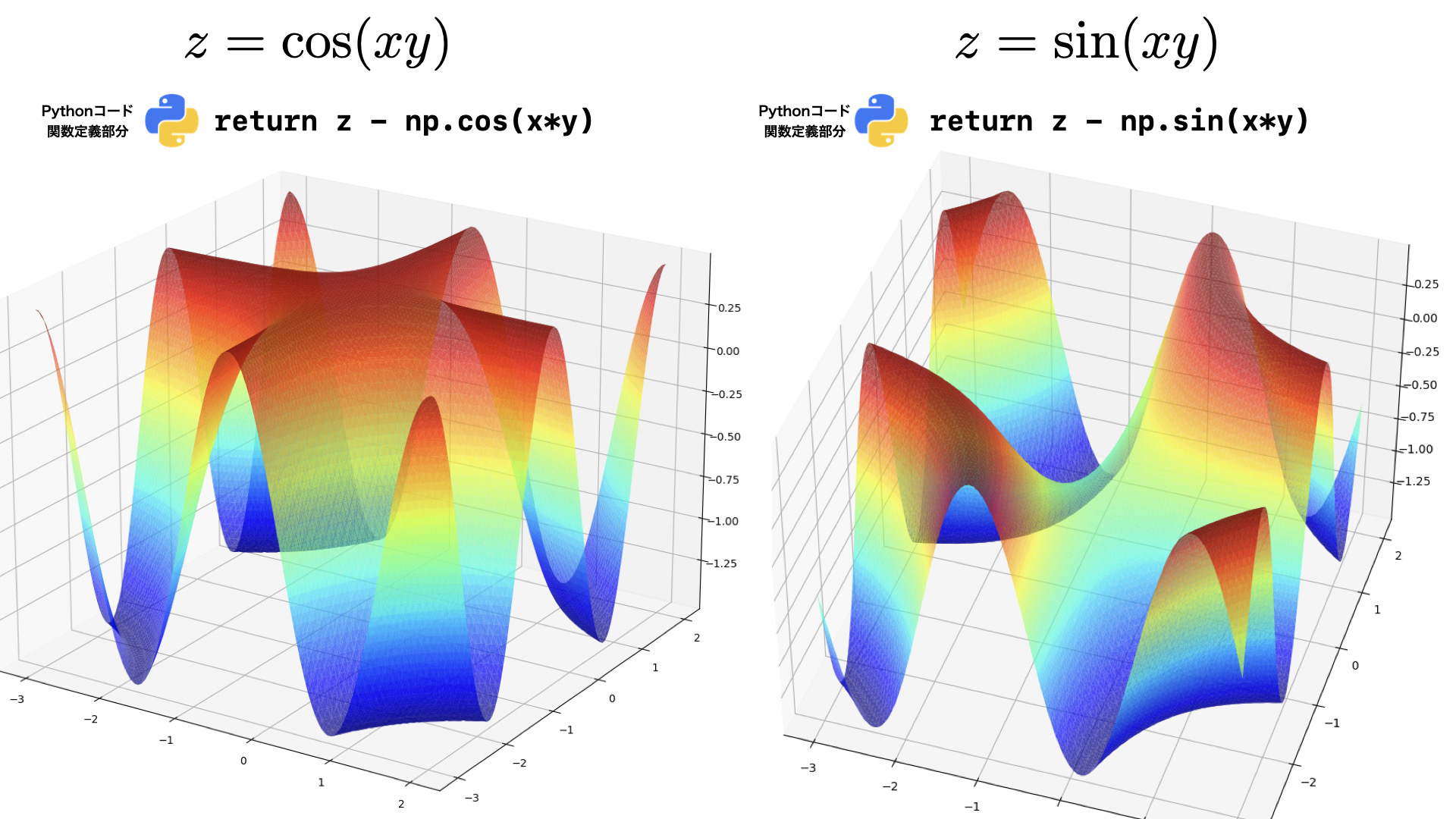
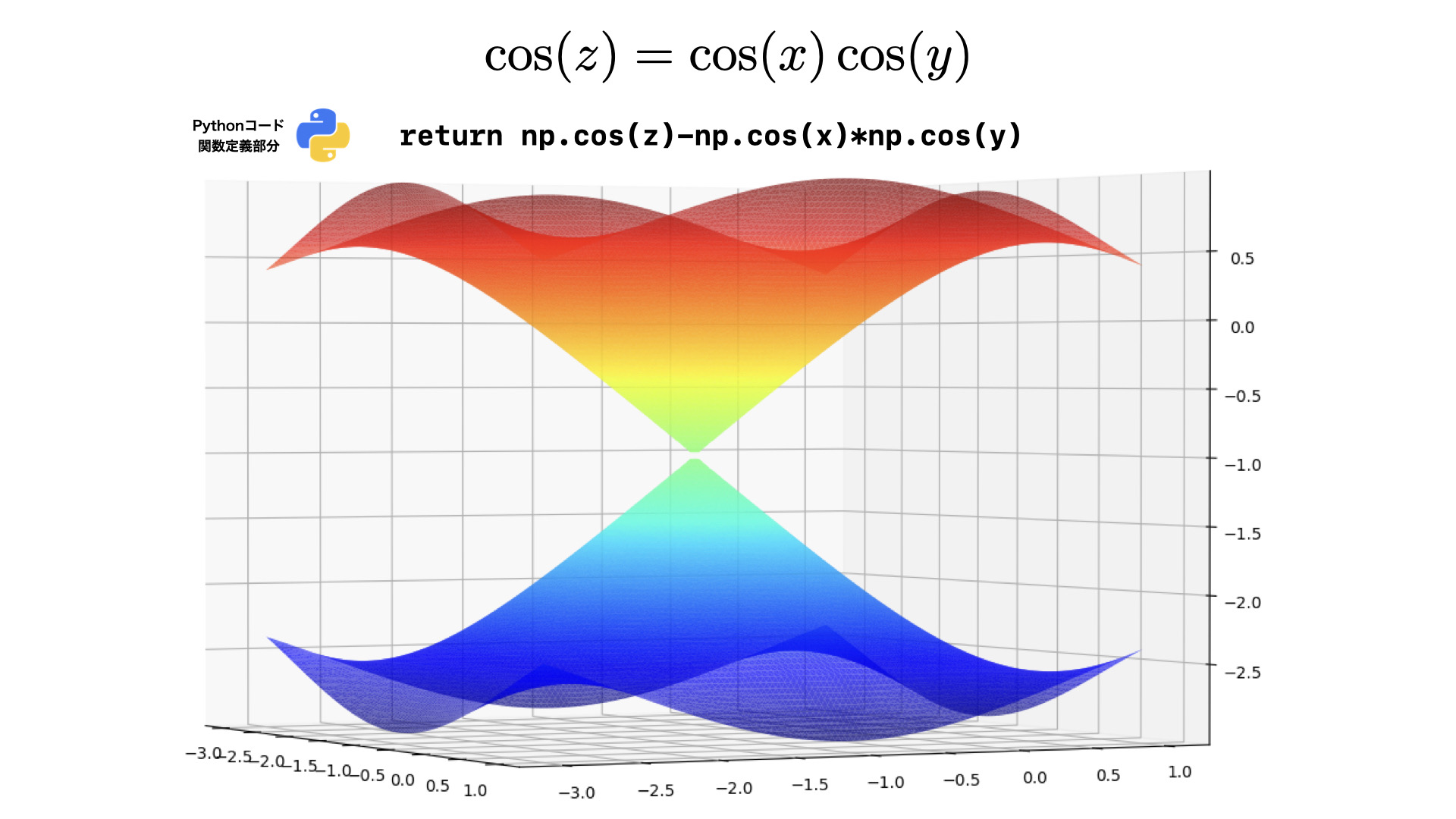
2D・3D
曲線・曲面
陰関数・パラメータ・極座標
グラフ描画用テンプレートを使ってコーディングのコツをマスター

■Peatix
http://ptix.at/6kGI8Q
小学生からわかる
超入門
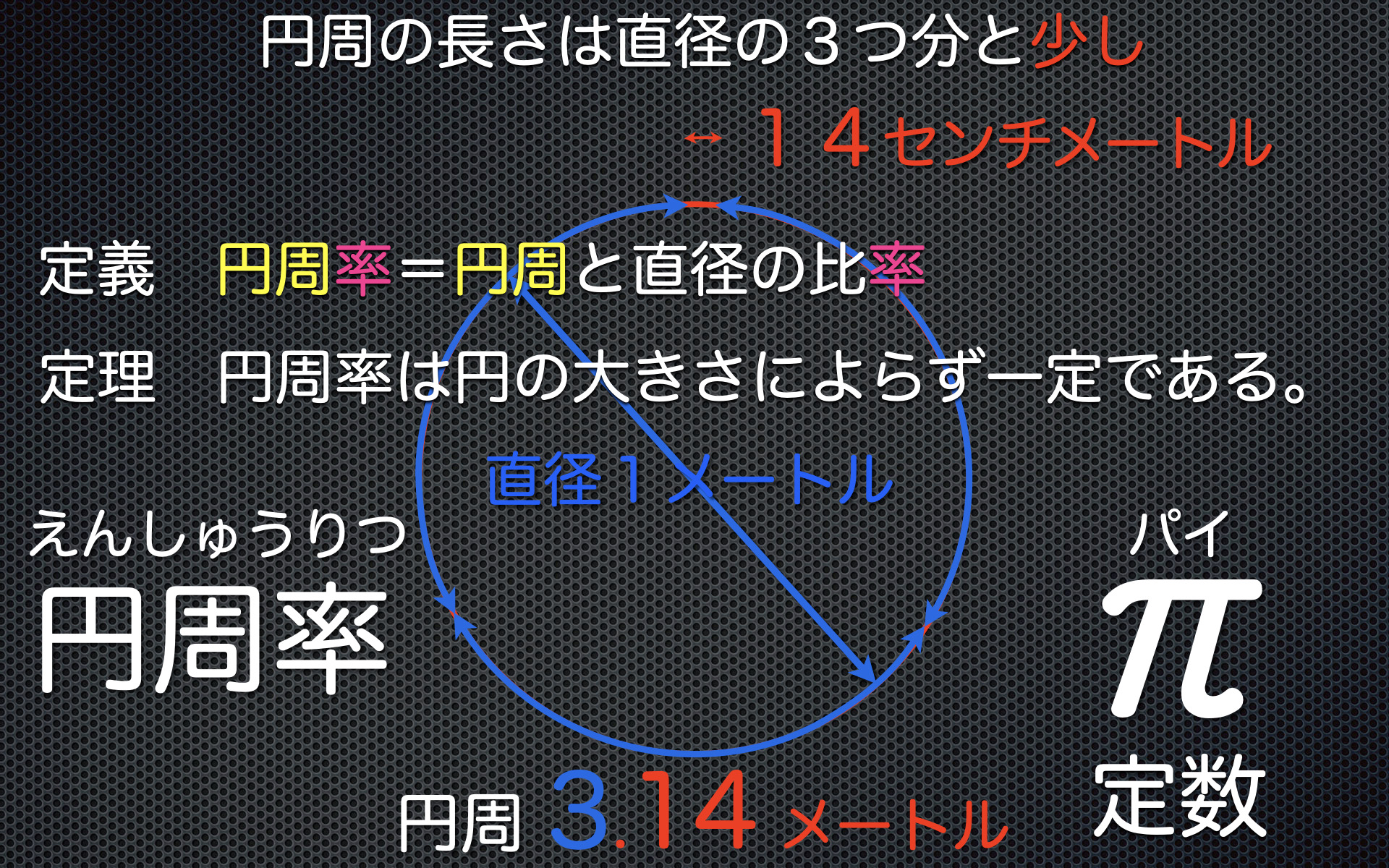
驚異の数円周率π
アルキメデスはいかにして3.14を求めたのか
みなが知っている円周率π=3.14…
しかし、その証明は東大入試にさえ出題されません
それほどに難しいということです
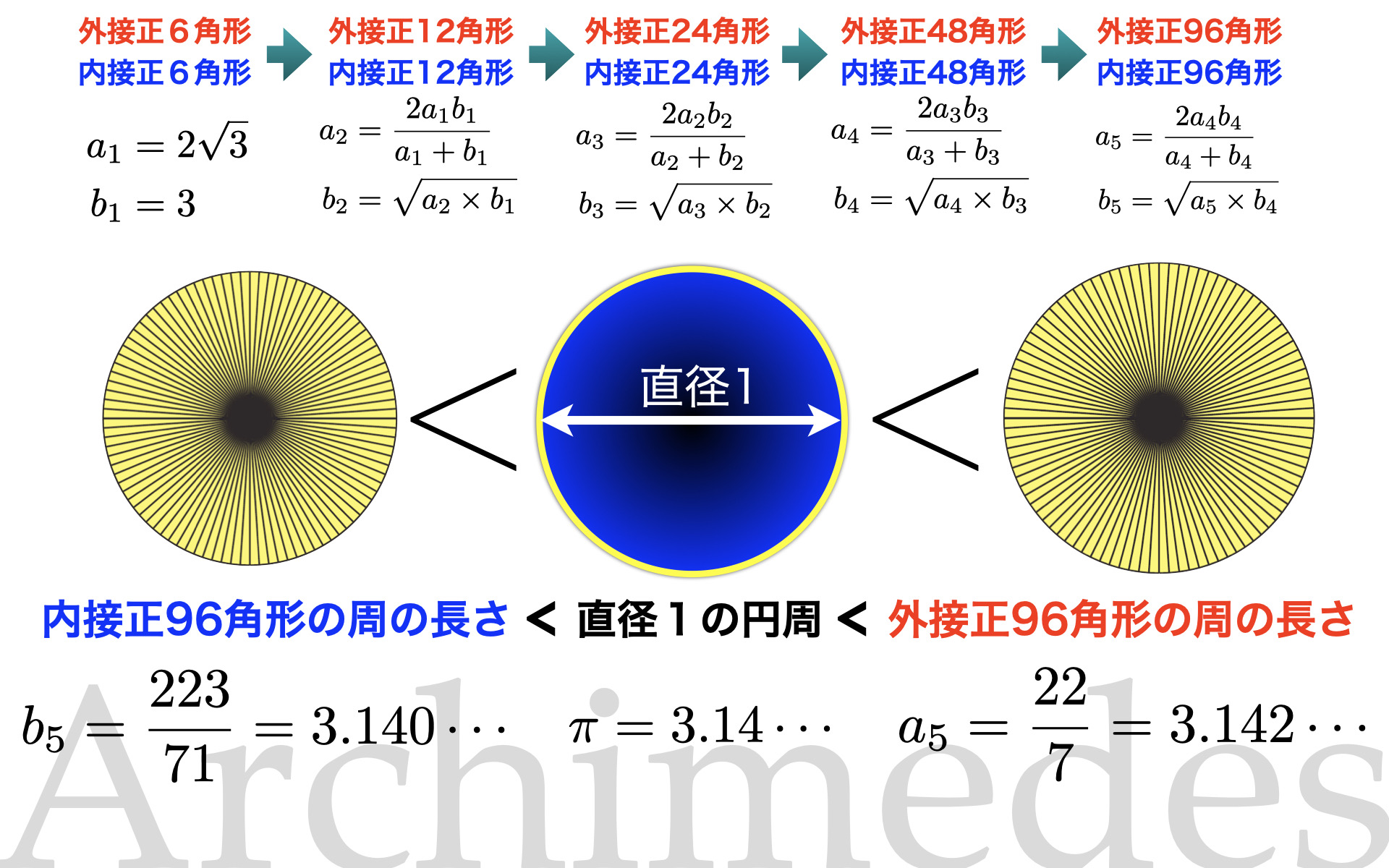
2300年前、古代ギリシャの数学者アルキメデスは
4000年前の古代エジプトで得られた3.1を3.14にアップデート
することに成功しました
アルキメデスの数学にせまります



申込Peatix
http://ptix.at/4vCBvn
小数点「.」誕生402年記念
驚異の数円周率π 2021
人はなぜπを計算しつづけるのか
2000年、サイエンスナビゲーターⓇに変身してから毎年アップデートした
πの物語を語りつづけてきました
2021年も万感をこめてサイエンスナビゲーターⓇはπを語ります







申込Peatix
http://ptix.at/G3xXUI
超入門・Pythonで
関・ベルヌーイ数
1712年関孝和
1713年ヤコブ・ベルヌーイ
に発表された関・ベルヌーイ数Bn
300年経った現在でも現在進行形
その一つが
算出アルゴリズムの発見
関・ベルヌーイ数算出Pythonコードをいくつも紹介します
・桜井進のコード
・Akiyama–Tanigawa algorithm
・B(n) is just sum of k^n formula linear term coefficient.
・Zeta function algorithm
1時間の授業で一気に総覧できるのも
電子計算機とPythonのおかげ
申込Peatix
http://ptix.at/KsZh4I
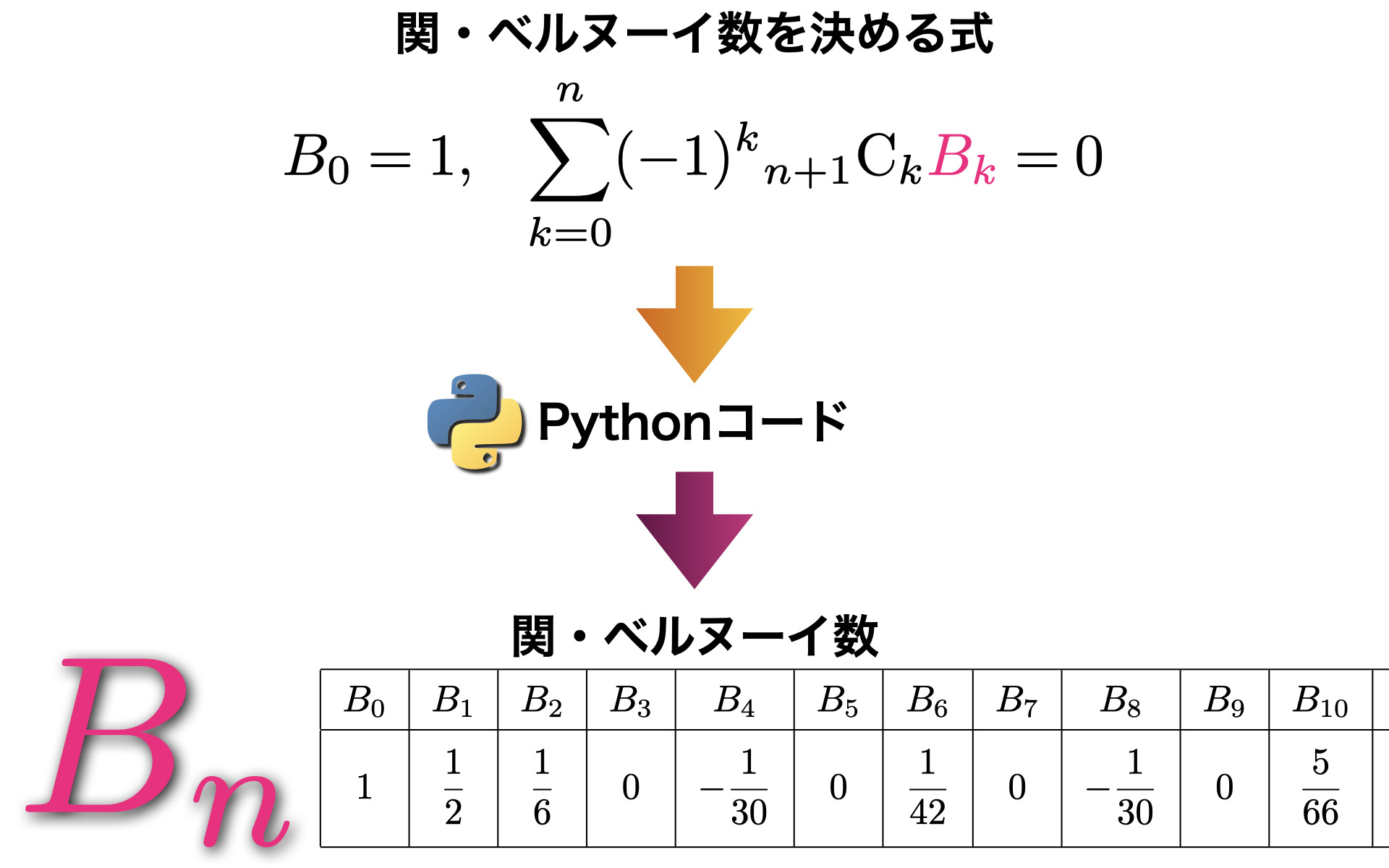
べき和公式、ゼータ関数など現れる関・ベルヌーイ数
関・ベルヌーイ数B(n)を算出するアルゴリズムをPythonに翻訳
結果をsympy.bernoulli(n)と比べてみます

■申込
Peatix 桜井進の算数・数学教室
(クレジットカード・コンビニATM・PayPal)
小学生からわかる
超入門
関・ベルヌーイ数
自然数のたし算に現れる関・ベルヌーイ数
300年前に日本人数学者関孝和によって発見
同時期にヤコブ・ベルヌーイによっても発見
関・ベルヌーイ数はフィボナッチ数と同じく数列
関・ベルヌーイ数を知る1時間
関・ベルヌーイ数を一度知ったら興味がどんどんわいてくることでしょう


■申込
Peatix 桜井進の算数・数学教室
(クレジットカード・コンビニATM・PayPal)
https://sakuraiclass.peatix.com/
スタディ中学受験情報局 [運営・管理] 株式会社バレクセル
【Web連載:数学と言葉】第2回
数の言葉使いその2 数と数字のちがい説明できますか
桜井進の算数・数学教室9月・10月共通テーマ
超入門・ゼータ関数

オイラー、計算の旅
18世紀、少年オイラーがスイスのバーゼルで知った問題
自然数の2乗の逆数の無限和はいくつになるか
10年に渡る計算の旅の末にたどり着いた終着駅
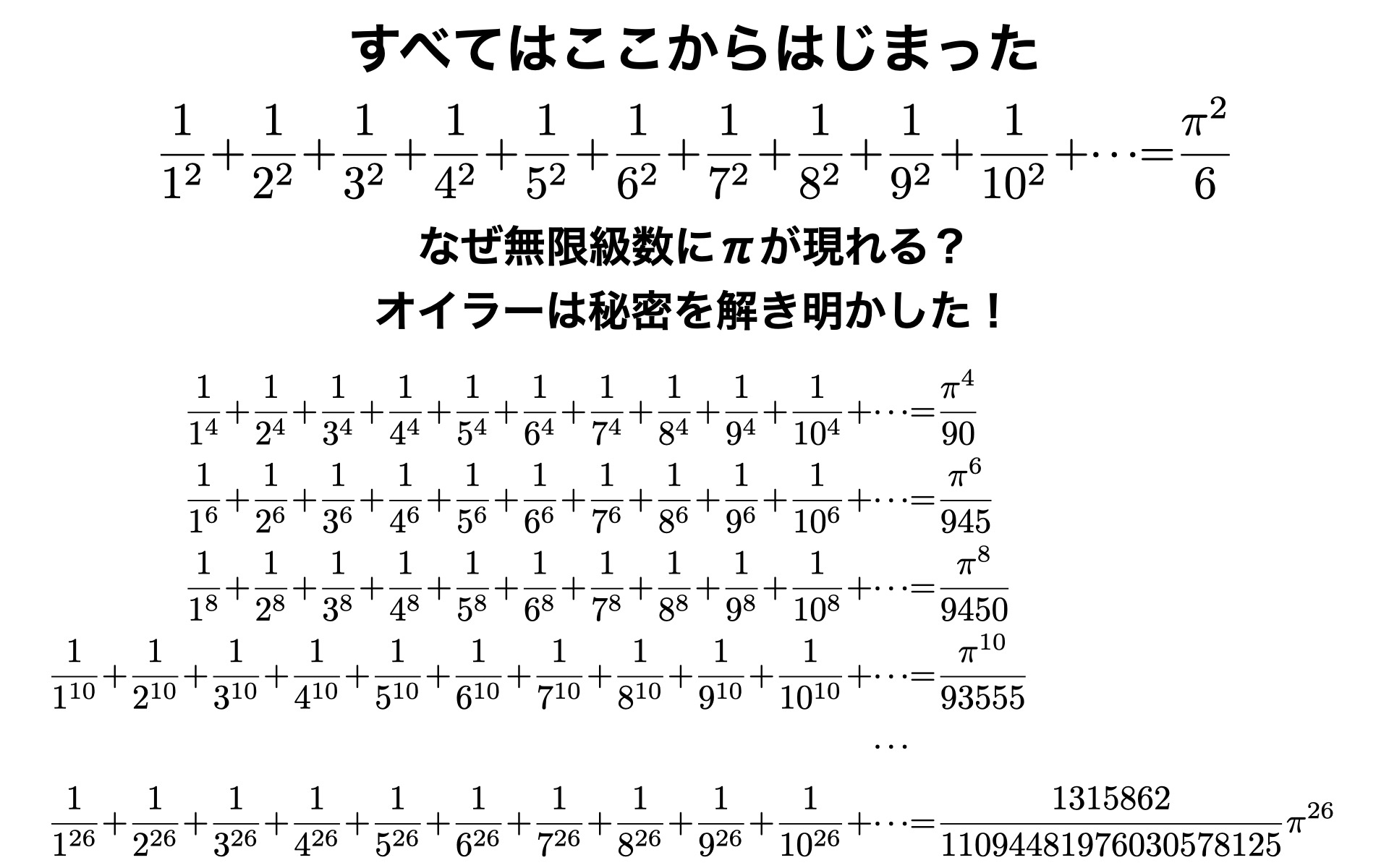
驚くべきことに円周率πが出迎えてくれた
なぜπが現れるのか
オイラーの挑戦はつづいた
証明の鍵は、三角関数、微分積分、そして対数
1735年、28歳のオイラーはその全貌を解き明かした
そして手にいれたのがゼータ関数

オイラーはここを始発駅として
あらたな計算の旅に出る
さらに驚きの風景がオイラーを待っていた

まさに数学はマジック!
無限にたし算できるマジック
数の世界のルールこそマジックのタネ明かし
数の世界に秘められた驚異のルールをオイラーの超絶技巧が解き明かす
数式美術館巡りをしましょう
たし算の驚きの風景に遭遇します
■Peatix
http://ptix.at/nj72nU