サイエンスナビゲーター(R)桜井進
■9/26(日)13:00-14:00 桜井進の魔法の算数教室 【小学生からわかる 超入門・ゼータ関数 オイラーの無限のたし算を鑑賞】
■9/26(日)14:30-16:30 桜井進の数学浪漫紀行 【超入門・ゼータ関数 オイラー、計算の旅】
■10/17(日)11:00-12:00 桜井進のPython・UNIX・Math教室 【Pythonでゼータを操る】
■10/24(日)13:00-14:00 桜井進の魔法の算数教室 【小学生からわかる 超入門・ゼータ関数 素数が無限にあることの証明】
■10/24(日)14:30-16:30 桜井進の数学浪漫紀行 【超入門・ゼータ関数 オイラーゼータからリーマンゼータへ】
■申込
桜井進の算数・数学教室の申込はPeatixに統一しました
□Peatix 桜井進の算数・数学教室
（クレジットカード・コンビニATM・PayPal）
https://sakuraiclass.peatix.com/
新連載 数学と言葉 スタート
スタディ中学受験情報局 [運営・管理] 株式会社バレクセル
第1回 数の言葉使いその1
「可能性は高い」それとも「可能性は大きい」
これまでの連載「人を数学する」に続いてテーマ一新、新連載がスタート
日本語の言葉使いを数学の視点から分析・考察
提案でも主張でもありません
言葉使い方にはルールが存在します
しかし、自然法則・数学法則ましてや法律のようなルールではありません
言葉を使うその人の判断で言葉は選ばれ
文字や音声になり人の外に放たれます
一度放たれた言葉はそれを見聞きする人に影響をあたえます
そうして言葉の世界はつくられていきます
本連載では国語では習わない言葉使いについて取り上げます。
数学と関わる言葉です。
連載予定
1. 「可能性は高い」それとも「可能性は大きい」
2. 数と数字のちがい説明できますか
3. 「かつ」と「または」
4. すべてと否定
5. 無理数とは何が無理!?
6. 数は「かず」それとも「すう」
オイラー、計算の旅
参加者 大人11名 子供1名
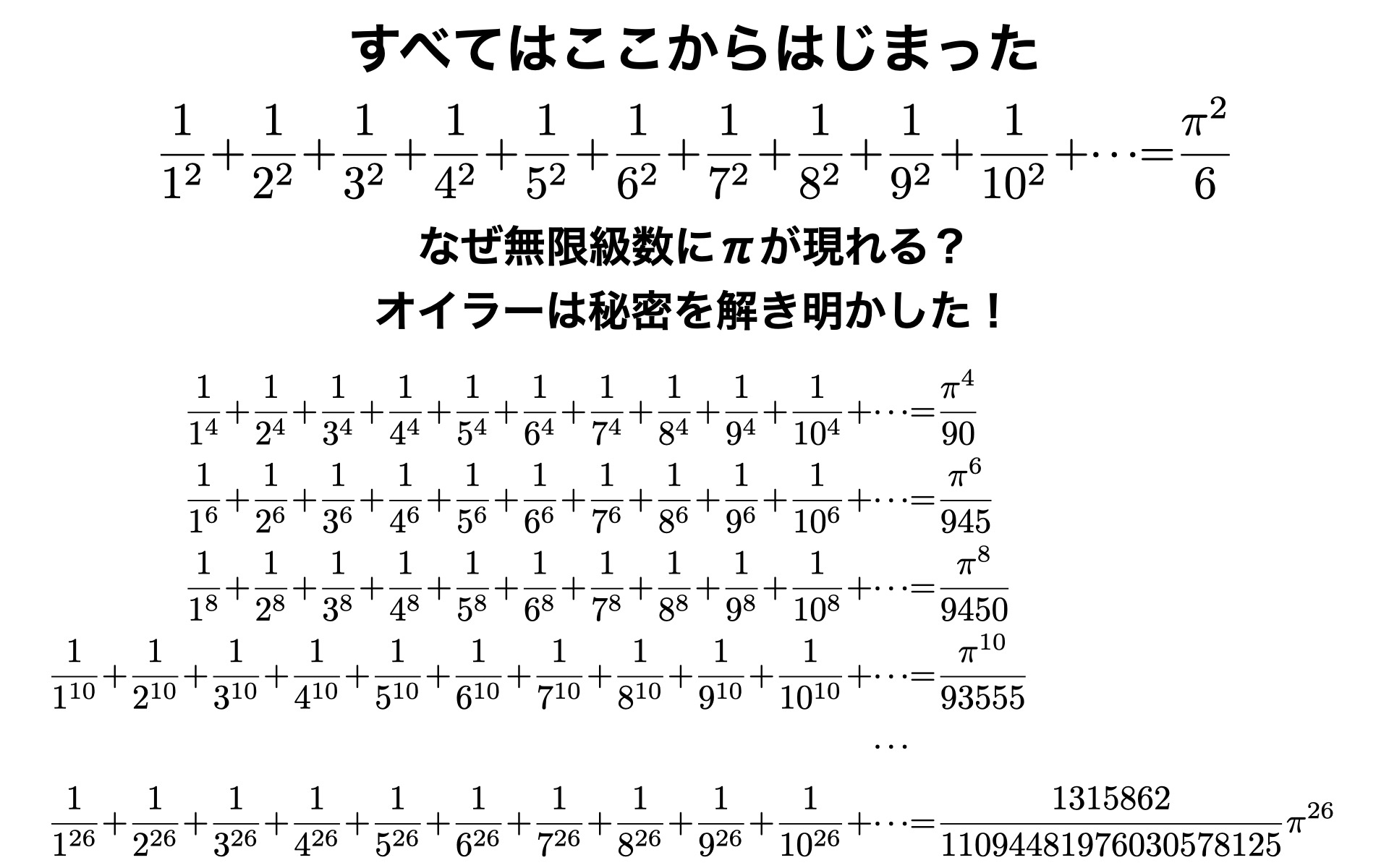
18世紀、少年オイラーがスイスのバーゼルで知った問題
自然数の2乗の逆数の無限和はいくつになるか
10年に渡る計算の旅の末にたどり着いた終着駅
\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^3}+\frac{1}{4^2}\cdots = \frac{\pi^2}{6}
驚くべきことに円周率πが出迎えてくれた
なぜπが現れるのか
オイラーの挑戦はつづいた
証明の鍵は、三角関数、微分積分、そして対数
1735年、28歳のオイラーはその全貌を解き明かした
オイラーはここを始発駅として
あらたな計算の旅に出る
さらに驚きの風景がオイラーを待っていた
1+2+3+4+5+6+7+8+9+10+11+\cdots =-\frac{1}{12}
まさに数学はマジック！
無限にたし算できるマジック
数の世界のルールこそマジックのタネ明かし
数の世界に秘められた驚異のルールをオイラーの超絶技巧が解き明かす
夏休み親子で数学
小学生からわくわく
級数！
無限の足し算にびっくり
参加者 6組（6歳・小1・小3・小4・小5）
テキスト 23ページカラーPDF（事前に送付・各自印刷）
2009年11月25日刊行
日本評論社 数学セミナー増刊
リーマン予想がわかる 黒川信重編著
巻頭31ページ・カラーが私の執筆
高校生からわかる
超入門・リーマン予想
最後は32ページ・33ページ「ゼータの100年後、リーマン予想解決へのロードマップ」でまとめた
これは私の予言である
いずれゼータに興味を持ち、解析接続を理解する小学生が現れると書いた
この予言は2019年であったが、2年遅れで小学生にゼータを語る時がやってきた
今回の授業はまさにその一環である
実は、これまでこの予言を叶えるためにいろいろと画策してきた
これからさらにそのプログラムを実行にうつしていく
テーマ
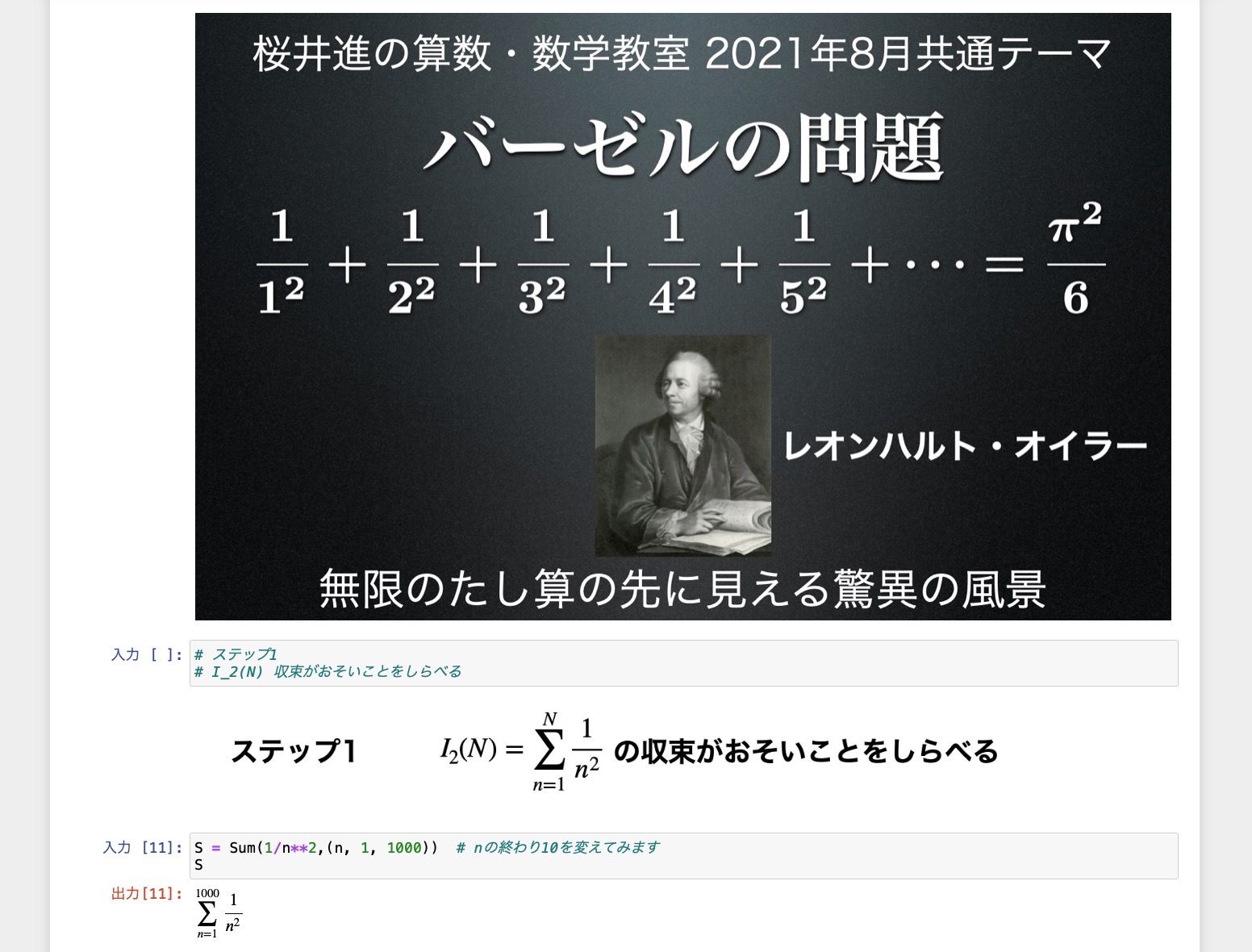
Pythonでバーゼルの問題
18世紀、スイスのバーゼル
14歳のオイラーは後にバーゼルの問題と呼ばれるようになる級数の問題を知る
師ベルヌーイ兄弟が解けなかった問題を少年オイラーは解くことを誓った
はたして、14年後28歳のオイラーは劇的に解いてみせた
10年以上に渡るオイラーの計算の旅を1時間で辿りました
紙とペンそしてPythonが動く電子計算機とともに
参加者 2名（小学4年生と大人）
■Pythonで素数シリーズ
1（5/16）素数生成
2（6/20）ゴールドバッハ予想
3（7/18）素数定理
4（8/22）バーゼルの問題
5 ユークリッドの証明（素数の無限性）
6 連続する合成数
7 ベルトラン=チェビシェフの定理
8 ルジャンドル予想
9 双子素数
10 素数の逆数の和
■テキストは紙テキスト（事前にPDF送付・各自印刷）jupyter notebookを使用
数学書でみると難解に見える数式たちもPythonの手にかかると数行のコードに変換
まさに、Pythonは新しい数学の教科書
さらにjupyter notebookはPythonコードの実行、実行結果を数式自然表示、画像挿入もできて
いうことなしのテキスト
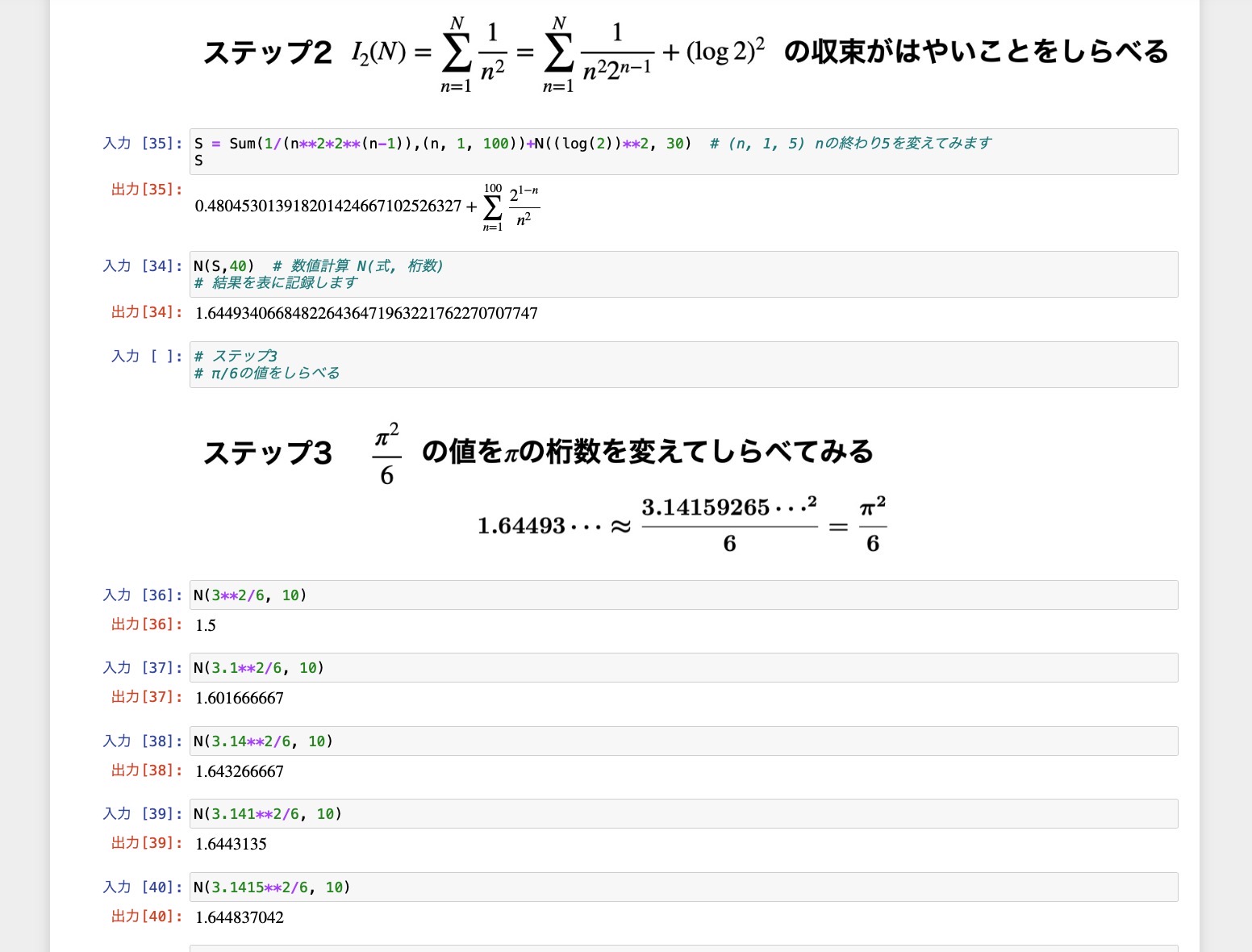
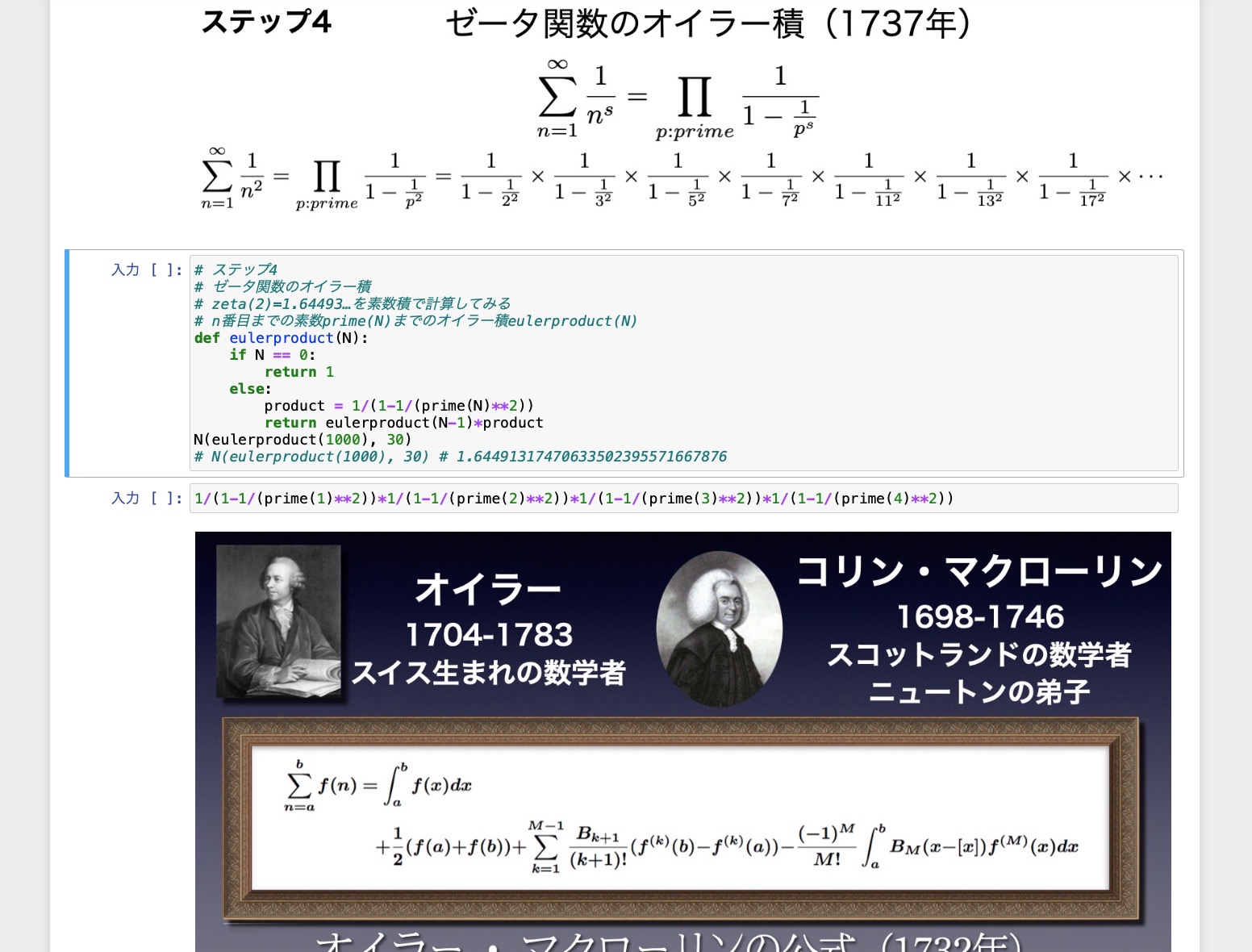
数値計算の結果を記録します
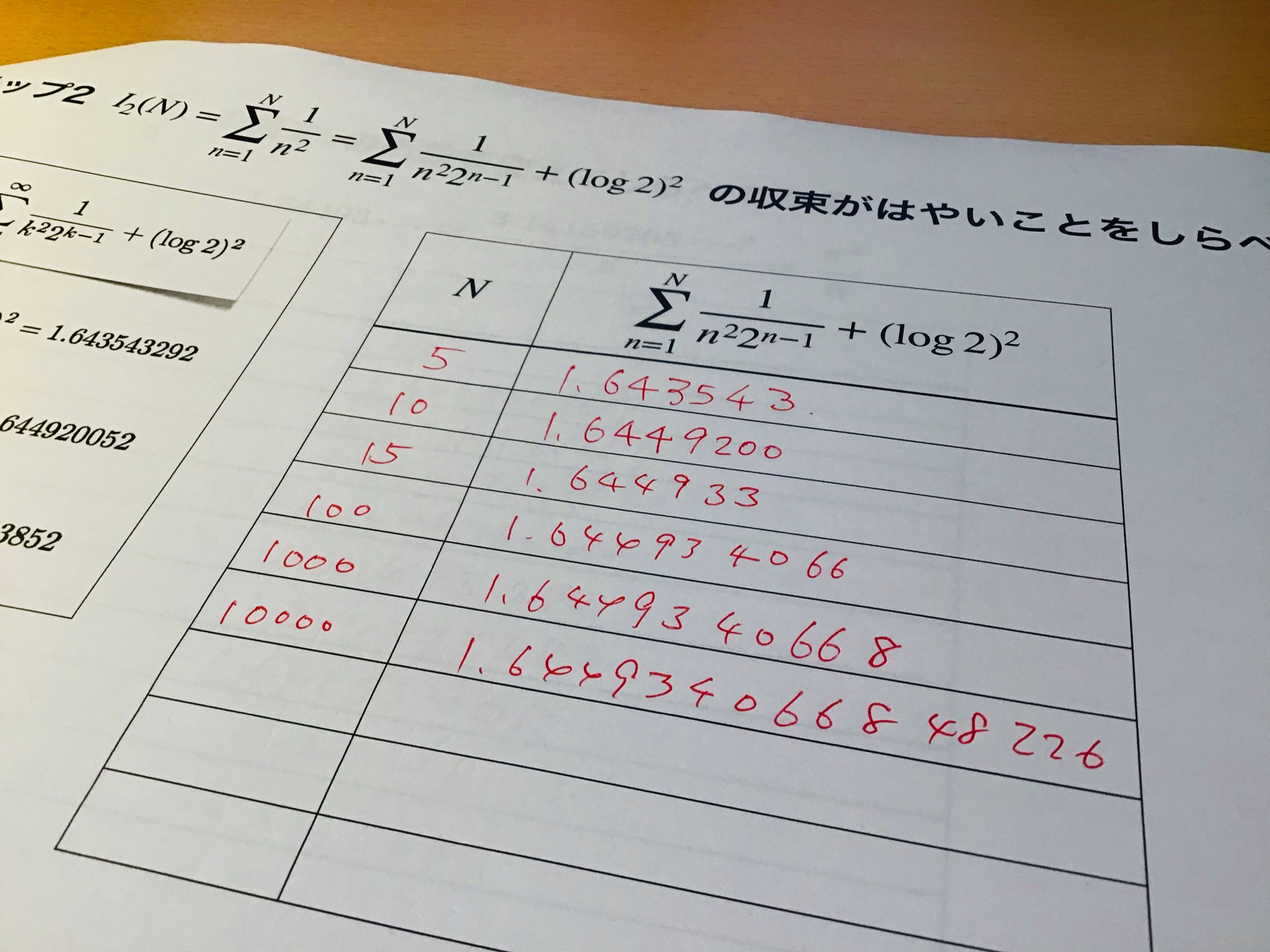
参加者 大人1名
ディープニューラルネットワーク
ディープラーニング
誤差関数
活性化関数
機械学習
テンソル
TensorFlow
Keras
画像認識の出力は確率
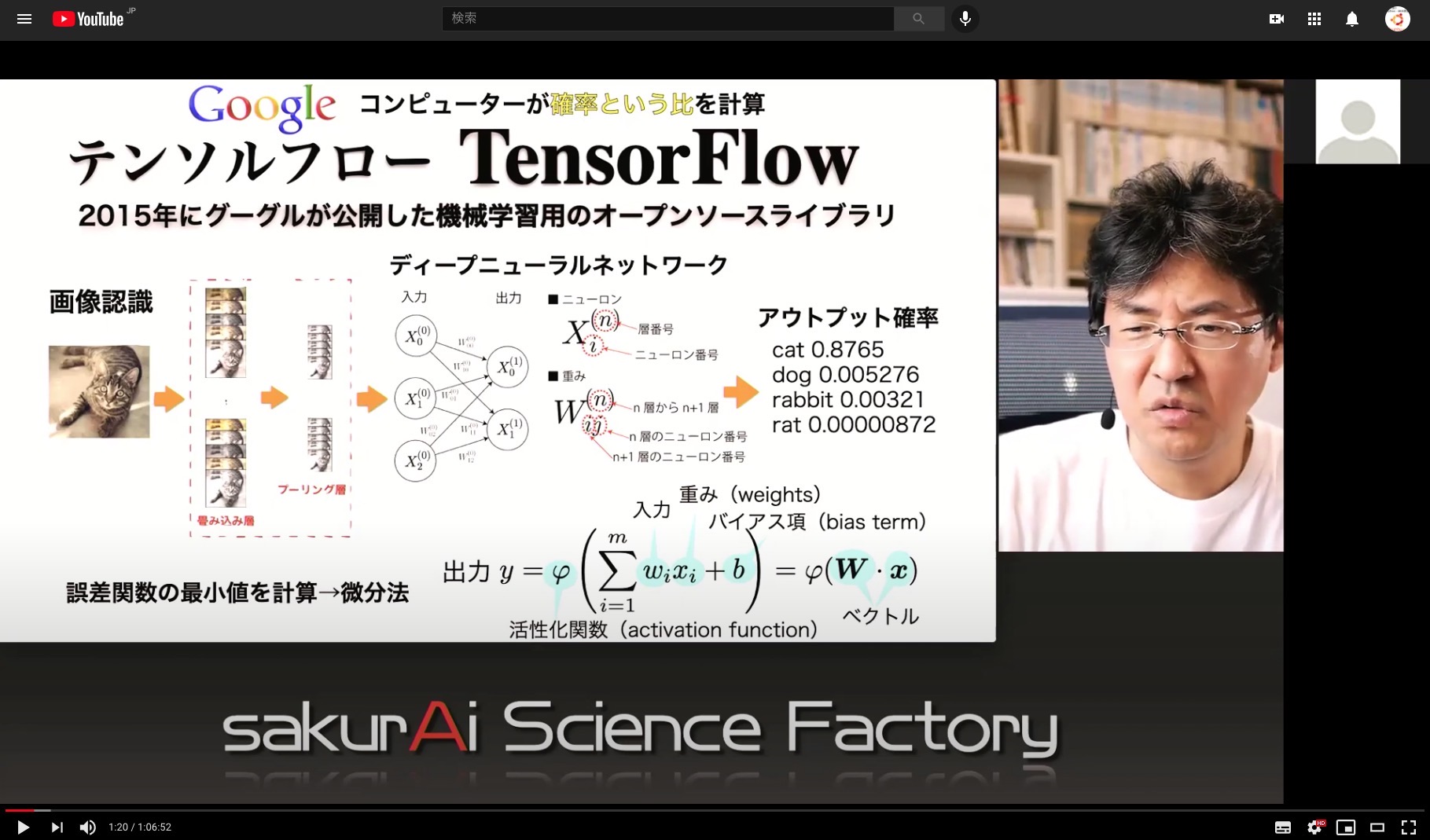
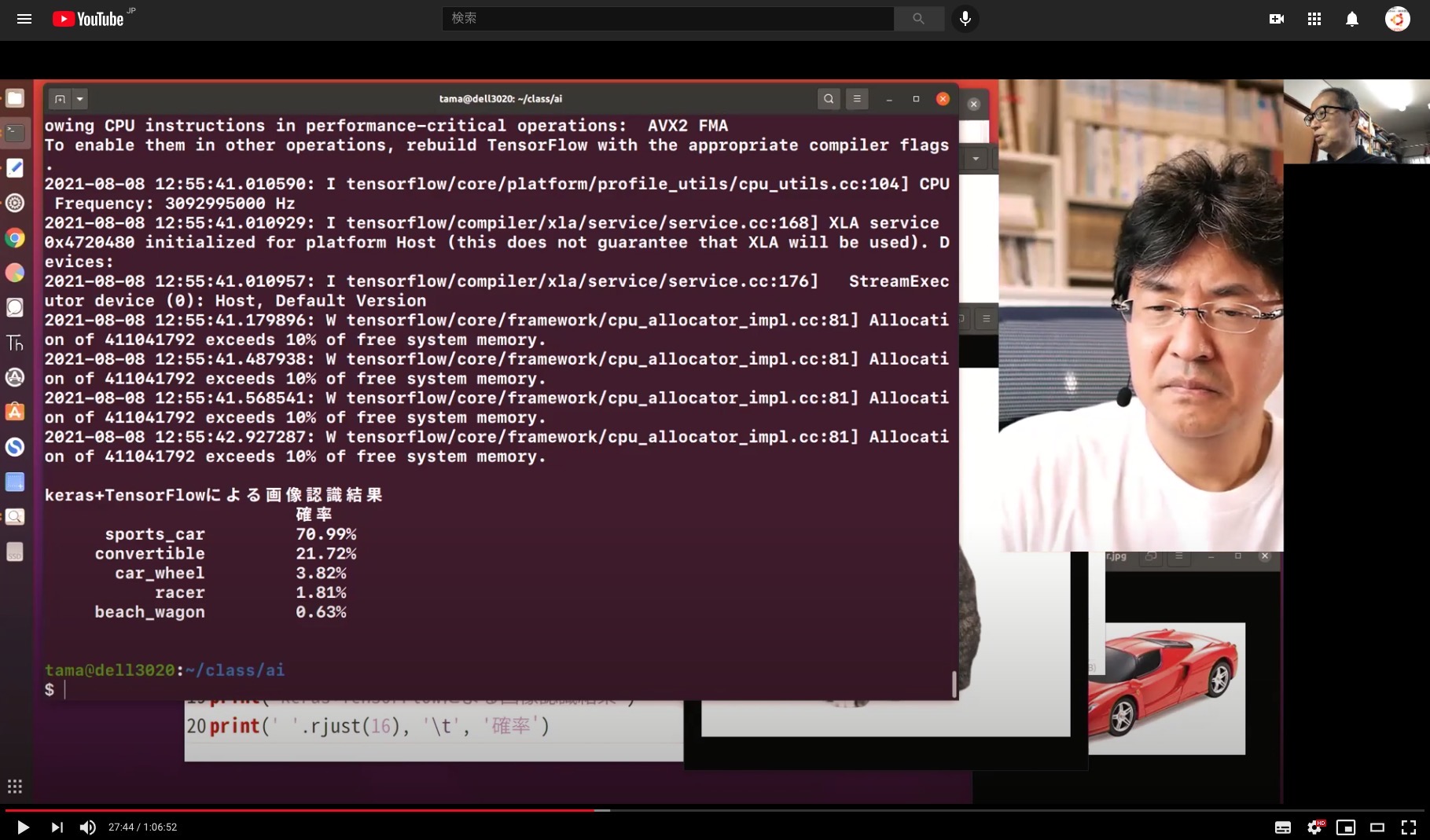
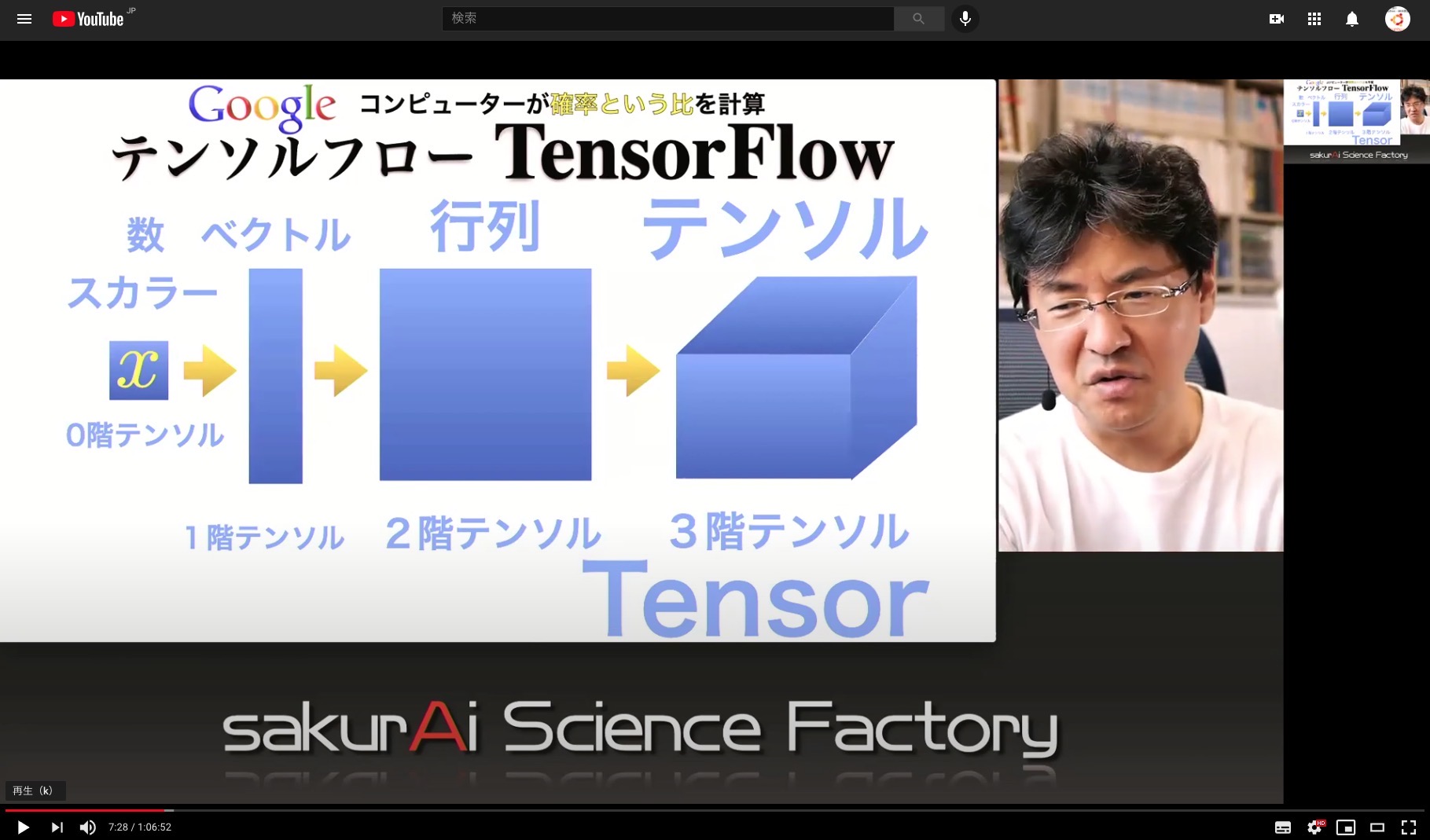
参加者 小学生2名
C言語、C++言語、LaTeX、Java、Perl、Ruby
Hwllo Worldプログラムのコンパイル
UNIXコマンドcd・lsのトレーニング
Python 素数判定プログラム
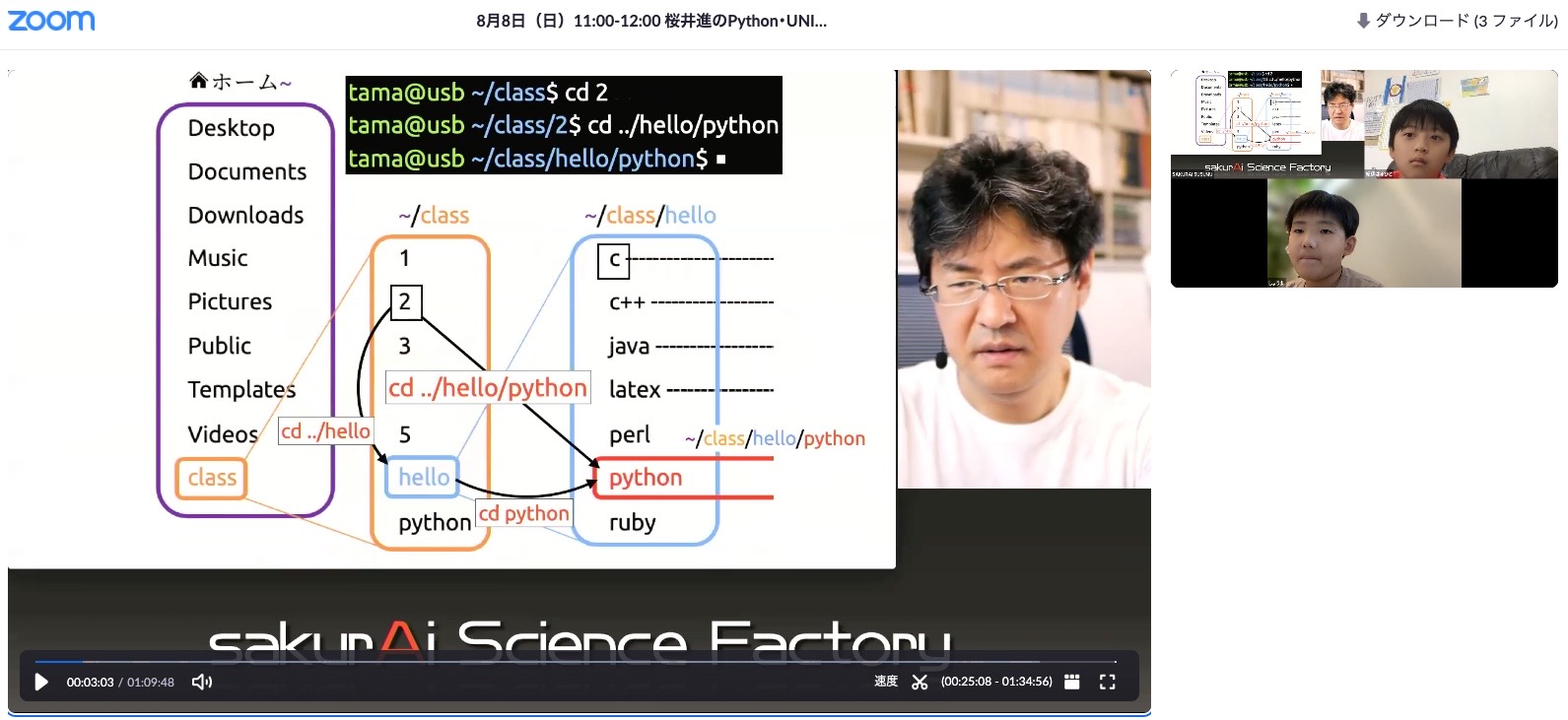
次回最終回第3回は
機械学習、ディープラーニング、画像認識、TensorFlow
好評連載中 空間情報クラブ
Pythonで数学を学ぼう！
第11回
Pythonで素数定理
■8/22(日)11:00-12:00 桜井進のPython・UNIX・Math教室
Pythonでバーゼルの問題
バーゼルの問題が素数に結びつく驚きの展開
■8/29(日)13:00-14:00 桜井進の魔法の算数教室
夏休み親子で数学
小学生からわくわく
級数！
無限の足し算にびっくり
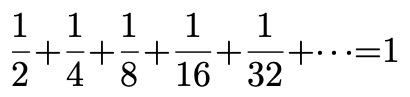
小学生にもわかるその仕組みにビックリ
円周率の正体も無限のたし算
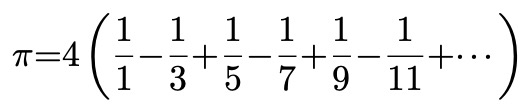
驚異の無限のたし算～級数～を知る・遊ぶスペシャルなひととき
■8/29(日)14:30-16:30 桜井進の数学浪漫紀行
オイラー、計算の旅
バーゼルの問題
18世紀、少年オイラーがスイスのバーゼルで知った問題
自然数の2乗の逆数の無限和はいくつになるか
10年に渡る計算の旅の末にたどり着いた終着駅
■申込
□桜井進の算数・数学教室Web申込フォーム（銀行振込・PayPal）
https://ws.formzu.net/fgen/S44553173/
□Peatix 桜井進の算数・数学教室（クレジットカード・コンビニATM・PayPal）
https://sakuraiclass.peatix.com/
小学生からはじめよう、対数！
5歳、小学２・３・４・５・６年生、10組参加いただきました
数学を知る
数学で遊ぶ
数学を使ってみる
どれも中学・高校の授業では体験できません
小学１年生からはじめましょう
対数とは何か
高校2年生で学びますが
高校3年生、大学生になっても実は「わかりません」
わからなくても使えるのです
わからなくても計算できます
a^x=yをx=にするのが対数
これは分かったうちには入りません
私がデザインした「かけ算ができる定規」「円型対数尺（画面に映っているカラフルな円）」
を切り取って使ってみると、ほんとうにかけ算ができることにビックリします
目盛りの間隔が不均一であることに気づきます
対数がわかる、とはこの間隔の不均一が納得できること
受験数学の高度な積分は対数を使います
対数の積分ができたとしても間隔の不均一を説明できる・納得するのは容易ではありません
、と5歳と小学生のみなさんに語りました
10年かけてその謎解きをしてごらんと
さらに
対数表をつかったかけ算の方法
私の16歳のときのジョン・ネイピアとの出会い
ジョン・ネイピア対数誕生物語
ジョン・ネイピア小数点「.」誕生物語
とつづきました
ちびっ子たちの心に残る1時間になったと思います
私にとっても思い出の授業になりました
■次回
8月29日(日)13:00-14:00桜井進の魔法の算数教室
小学生からはじめよう
級数！
無限の足し算にびっくり
1/2+1/4+1/8+1/16+… = 1
小学生にもわかるその仕組みにビックリ
円周率の正体も無限のたし算
π = 4 × ( 1-1/3+1/5-1/7+1+9-1/11+…)
驚異の無限のたし算〜級数〜を知る・遊ぶスペシャルなひととき
