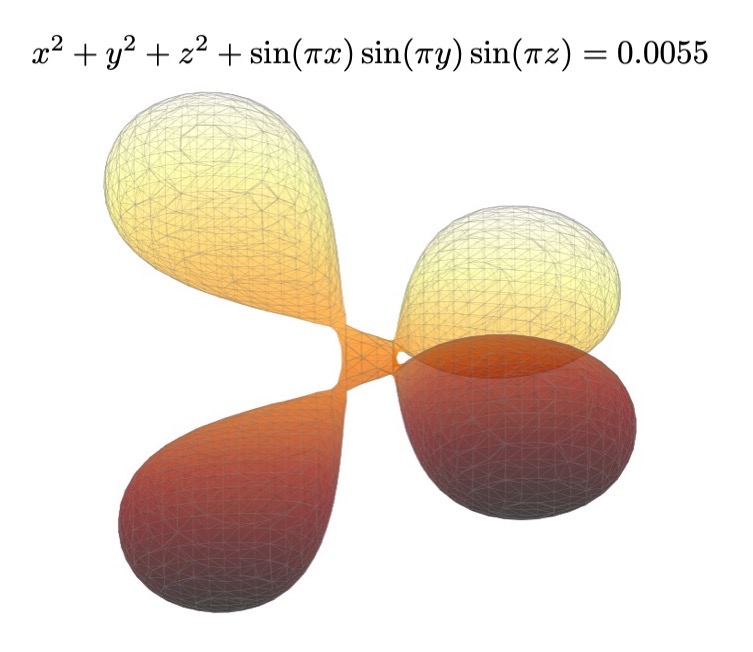
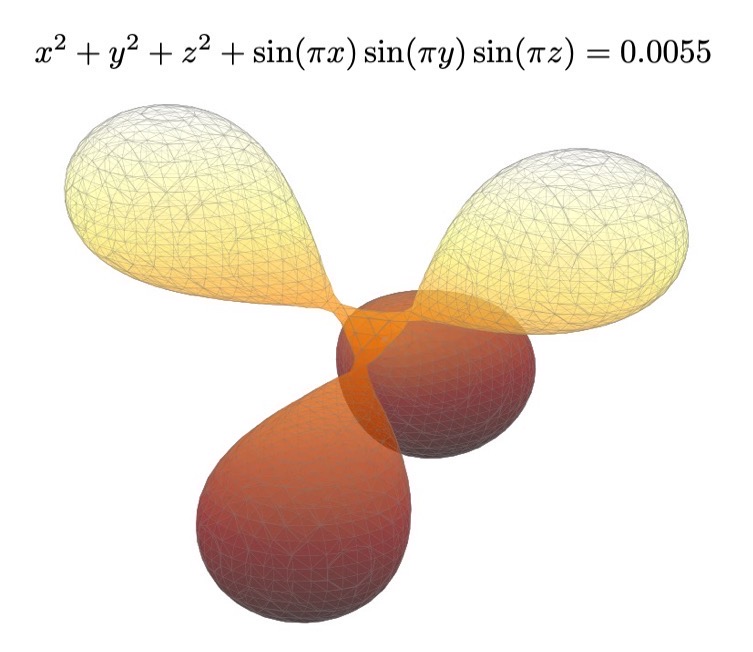
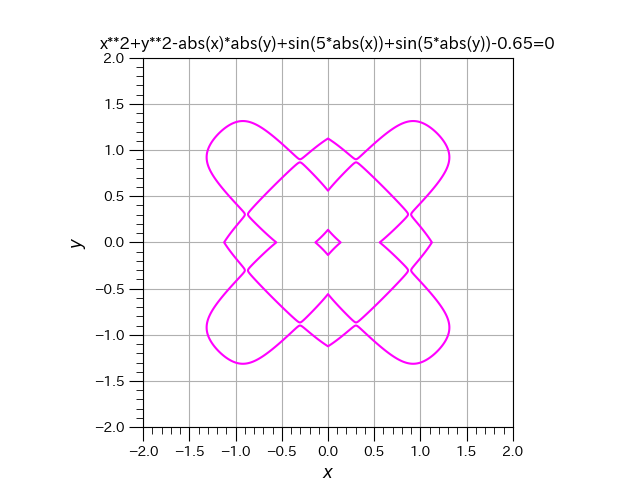
3/31 Zoomオンライン
1300-1400桜井進の魔法の算数教室
1430-1630桜井進の数学浪漫紀行
にて
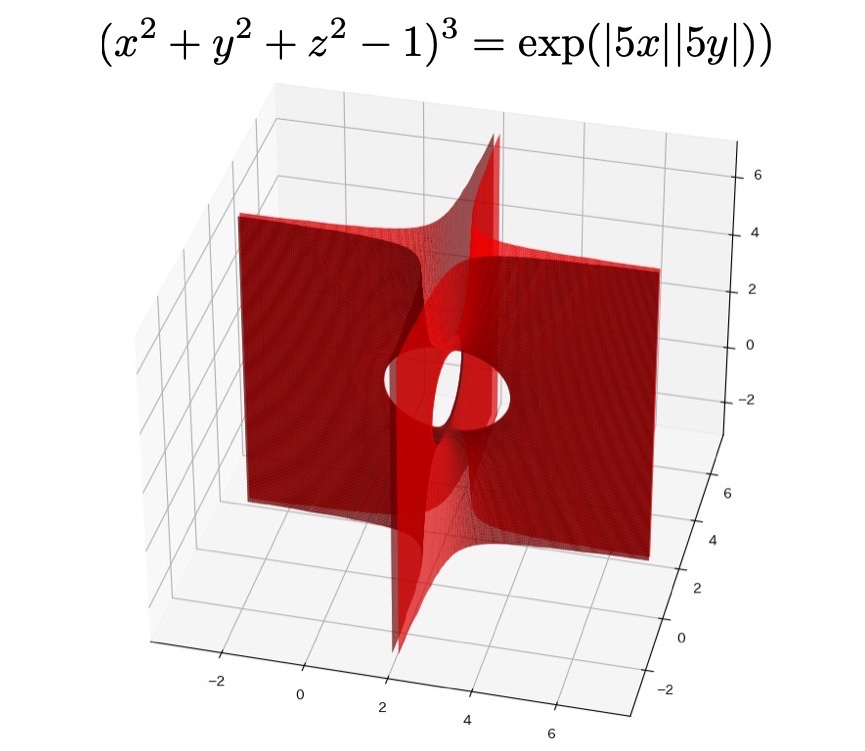
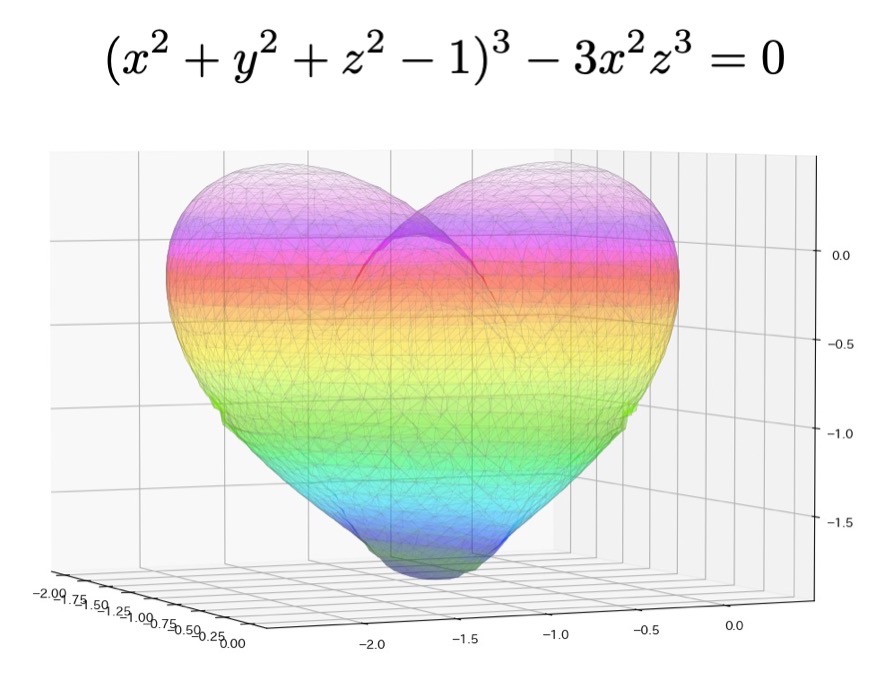
第3回 一行数式グラフコンテスト
を開催しました
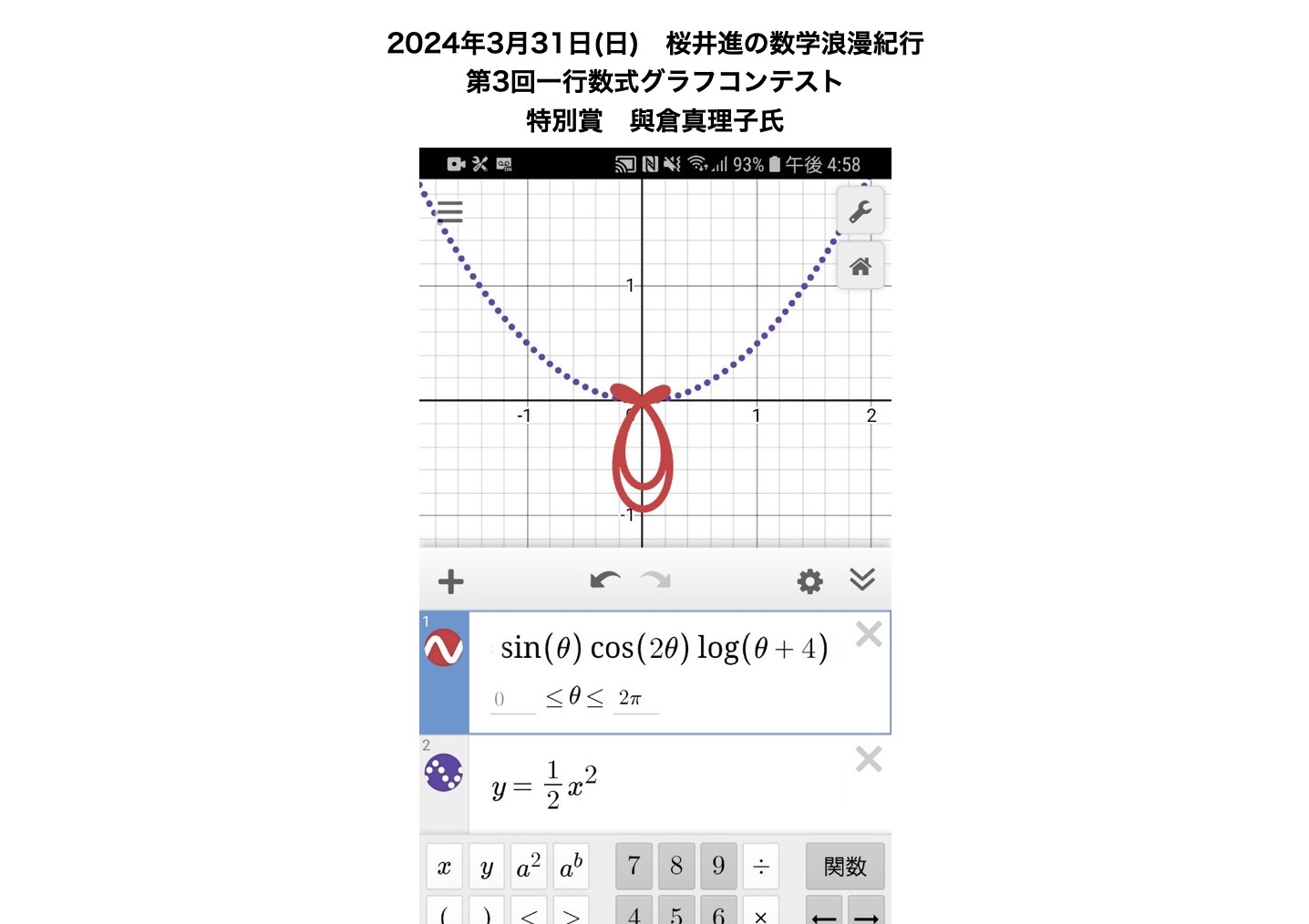
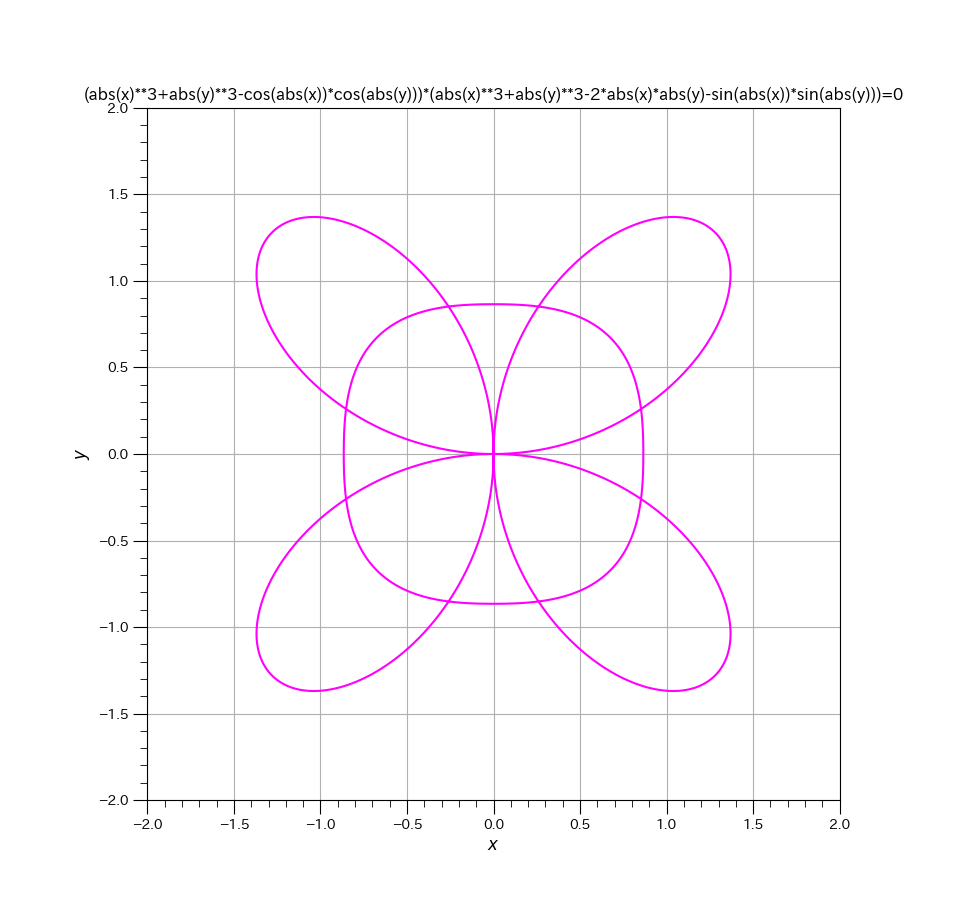
今回特別賞に選ばれたのは、與倉真理子氏の作品「ペンダントヘッド」
ネックレスの部分と合わせると2行になるので特別賞としました
ペンダントヘッド部分だけでも十分評価できる面白い作品です
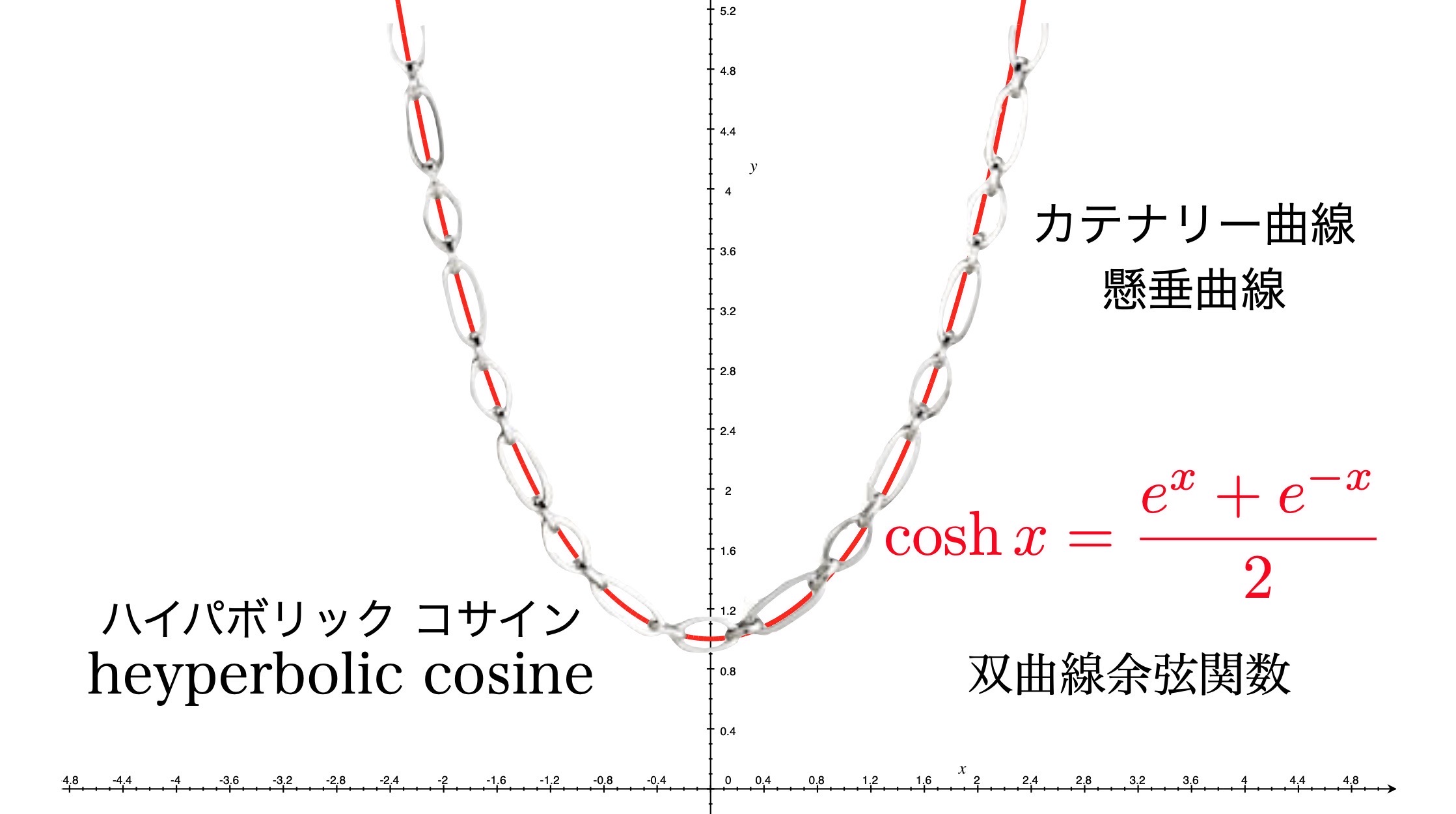
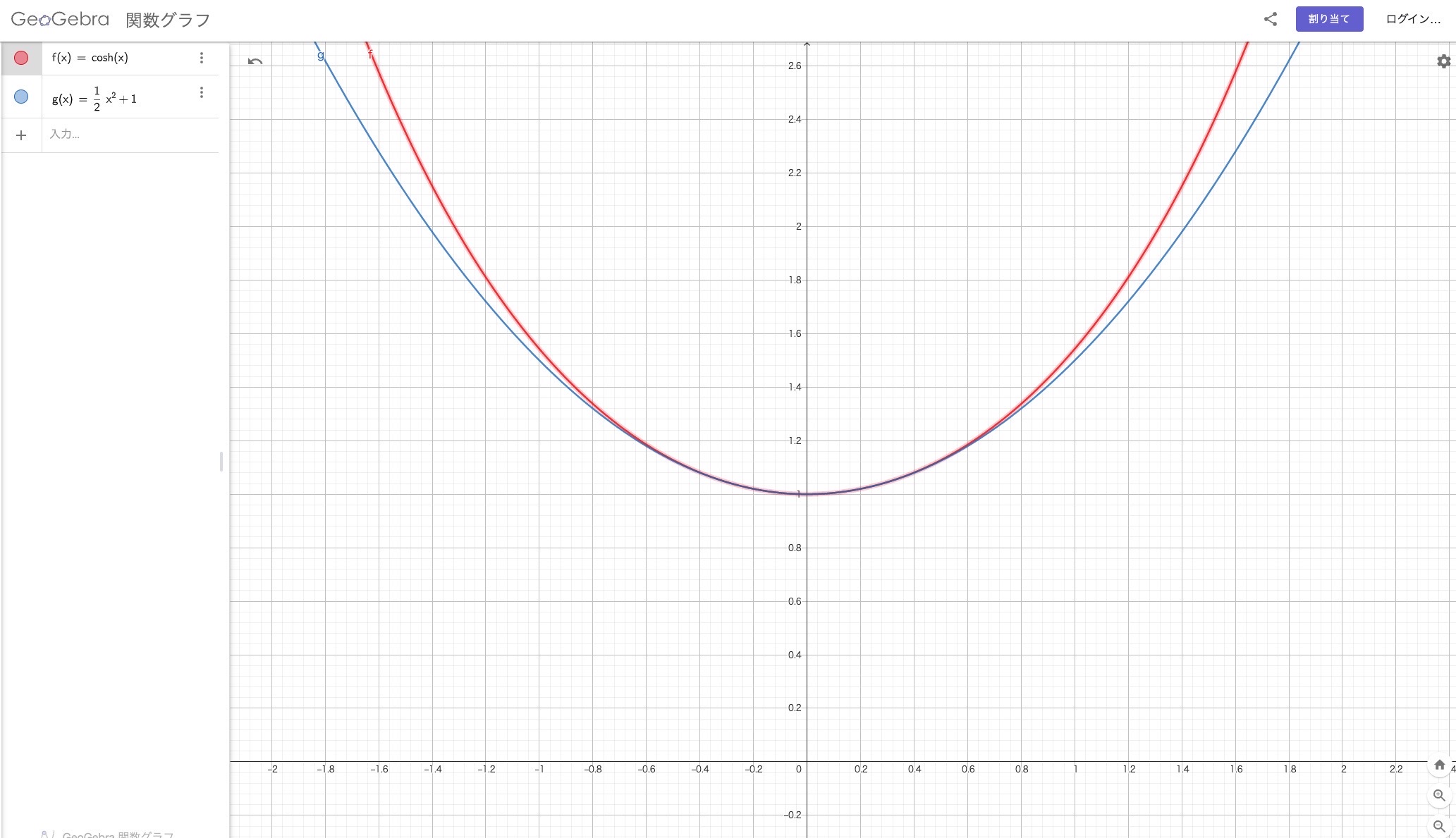
ちなみに、ネックレス部分は正確には放物線ではなく懸垂曲線(カテナリー)です
これを與倉氏は放物線 y=\frac{1}{2}x^2としました
カテナリーと放物線を比べてみると原点付近ではいい近似であることがわかります
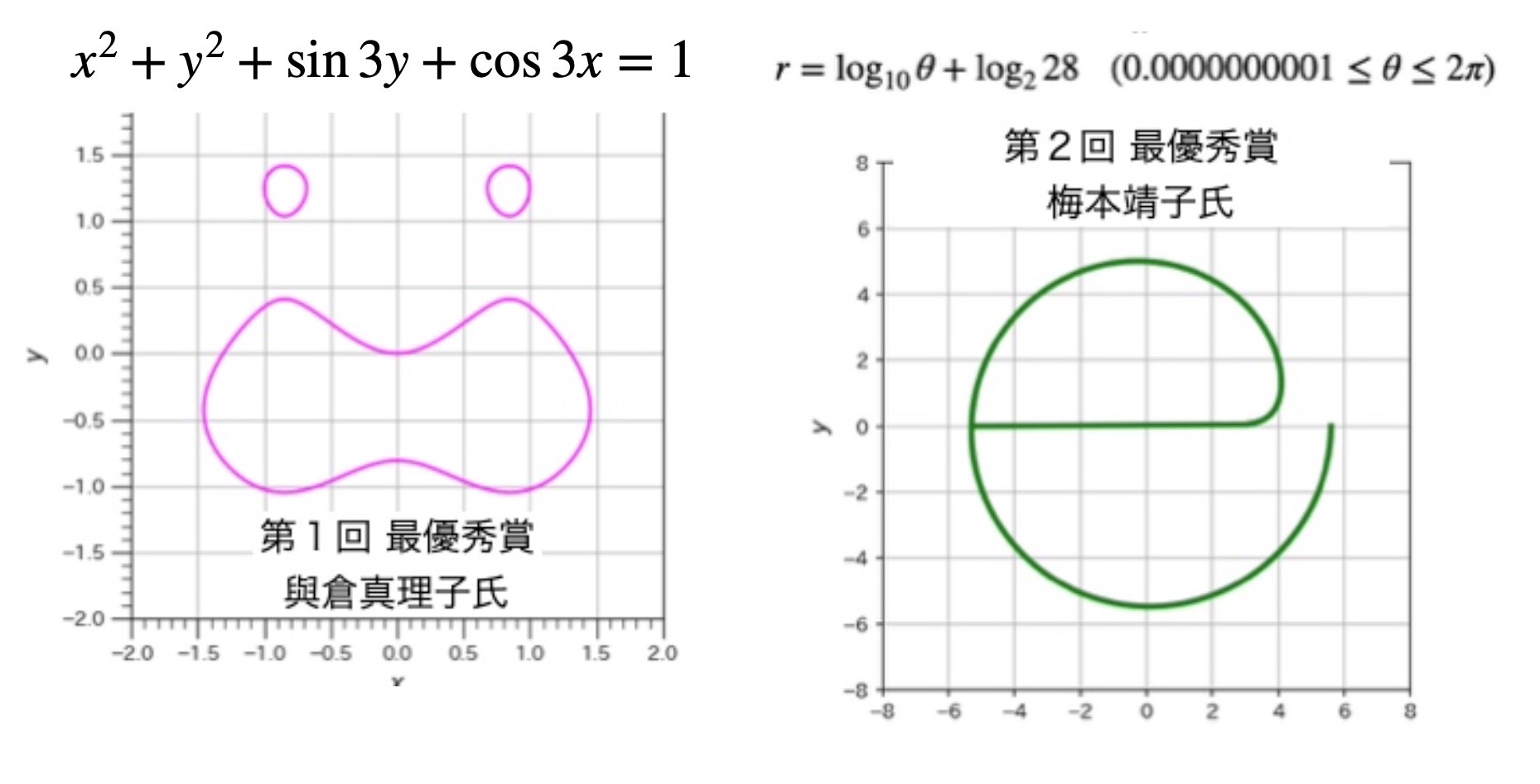
これで一行数式グラフコンテストは3回を数えました
過去の作品のような秀逸な作品は容易にデザインできません
そこで、次回からは
一行数式グラフコンテスト
に加えて
GeoGebra作品コンテスト(数式は何本でもOK)
もあわせて行おうとおもいます
これは世界中で開催されておりアート作品級に仕上げることができます
それを知っていたので、一行数式グラフコンテストを始めてみたのですが
グラフはいくらでもデザインできても面白いものをデザインするのが難しいのです
次回は1年後に開催予定
第4回 数式グラフコンテスト
・一行数式グラフ部門
・GeoGebra作品部門